Neravnomjerno raspoređeno opterećenje. Distribuirano opterećenje

Površinske i zapreminske sile predstavljaju opterećenje raspoređeno na određenu površinu ili zapreminu. Takvo opterećenje je dato intenzitetom, koji je sila po jedinici nekog volumena, ili neke površine, ili neke dužine.

Posebno mjesto u rješavanju niza praktično zanimljivih problema zauzima slučaj ravno raspoređenog opterećenja primijenjenog duž normale na određenu gredu. Ako usmjerite os duž grede 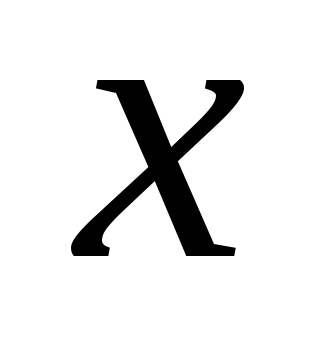, tada će intenzitet biti funkcija koordinata 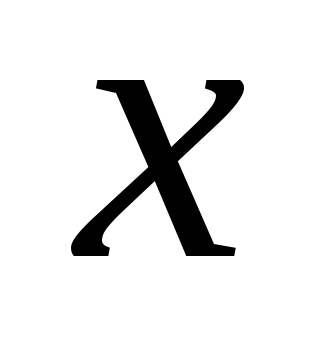i mjeri se u N/m. Intenzitet je sila po jedinici dužine.

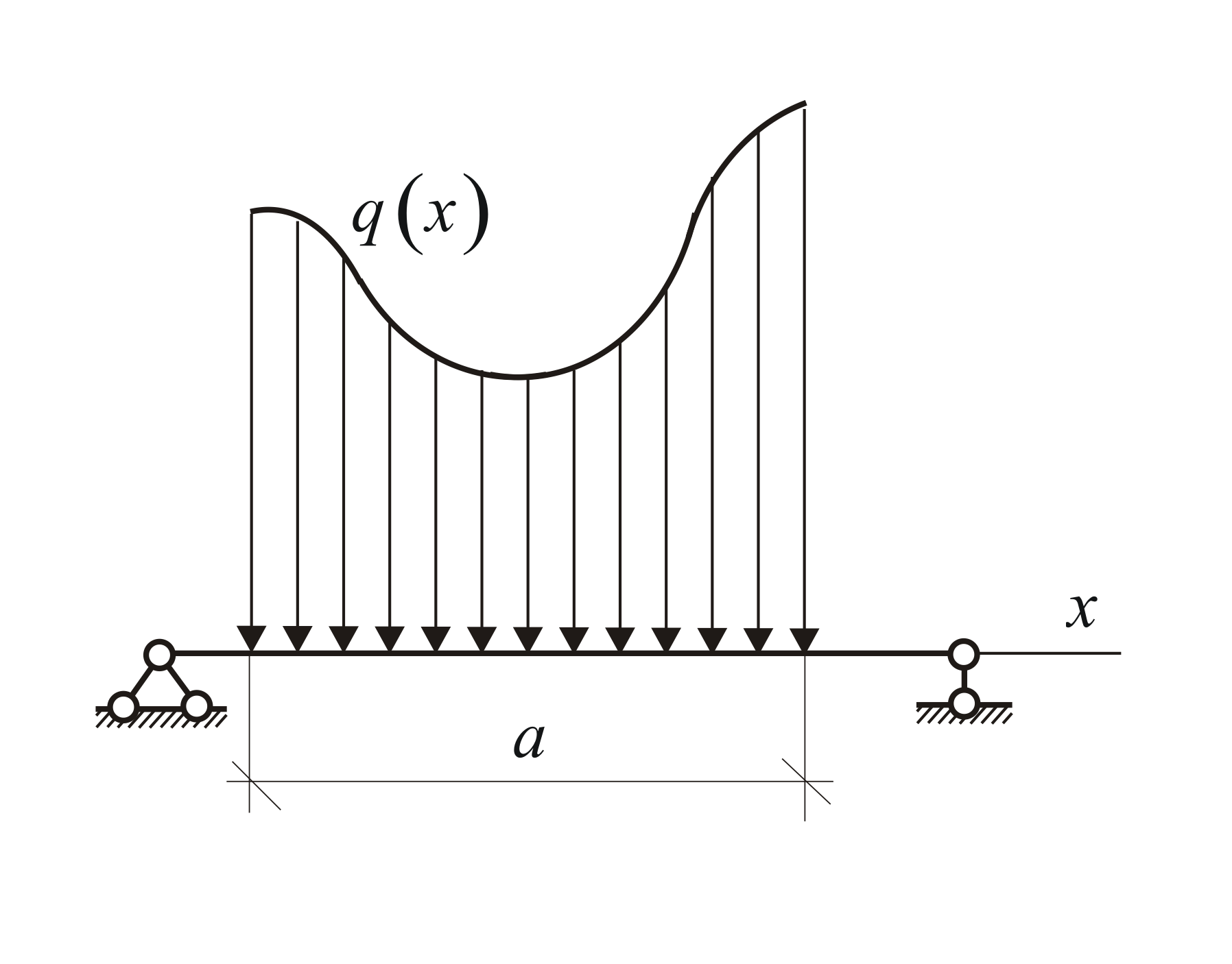
Ravna figura omeđena gredom i grafikom intenziteta opterećenja naziva se dijagram raspodijeljenog opterećenja (slika 1.28). Ako se po prirodi problema koji se rješava deformacije mogu zanemariti, tj. Budući da se tijelo može smatrati apsolutno krutim, tada se raspoređeno opterećenje može (i treba) zamijeniti rezultantom.

Podijelimo snop na dužine segmenta

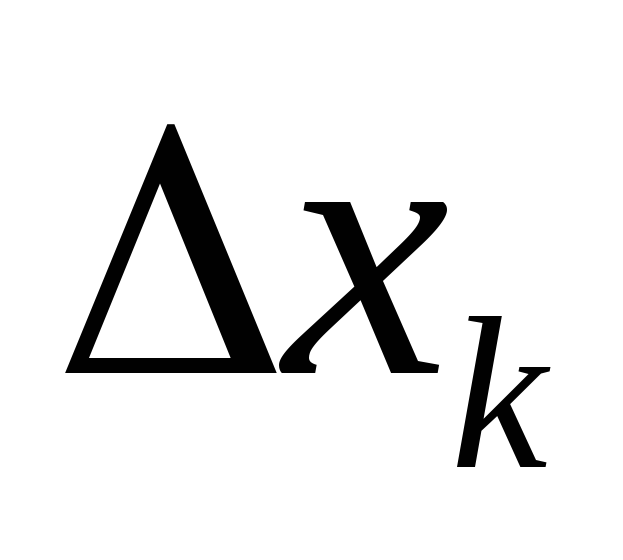, na svakom od kojih pretpostavljamo da je intenzitet konstantan i jednak

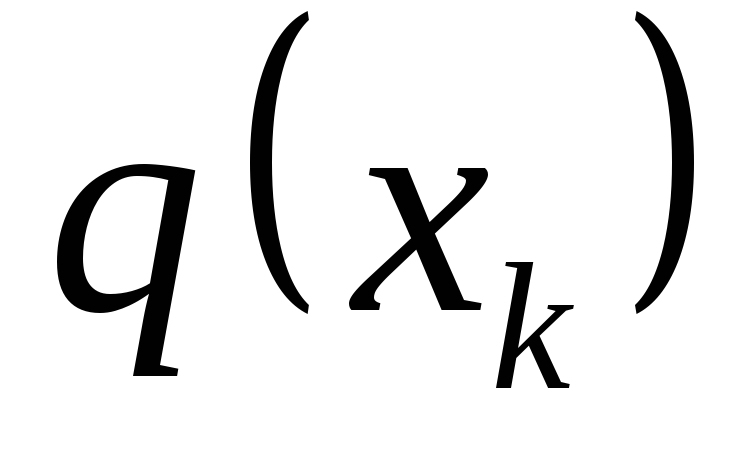, gdje 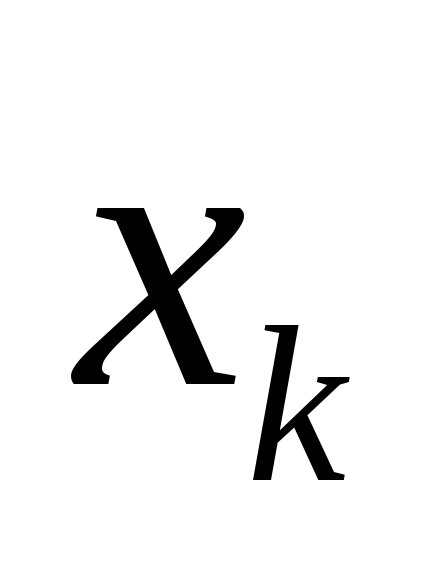- koordinata segmenta

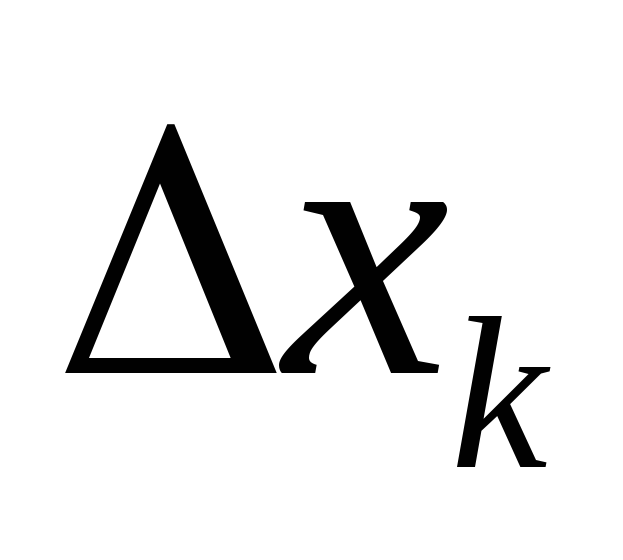. U ovom slučaju, kriva intenziteta je zamijenjena isprekidanom linijom, a opterećenje po segmentu

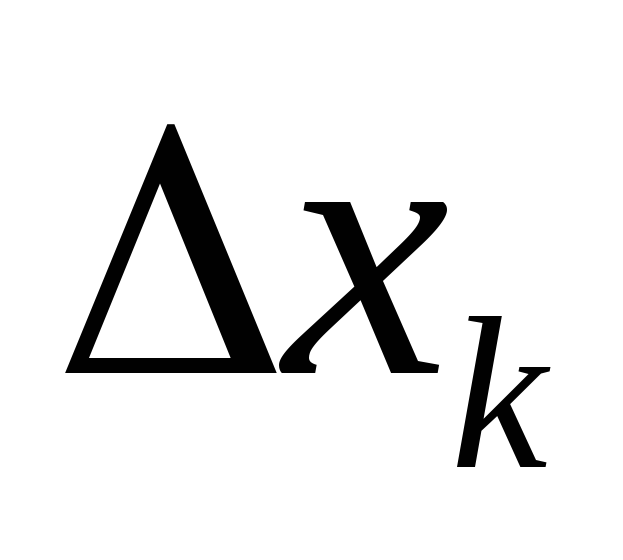, zamjenjuje se koncentrisanom silom

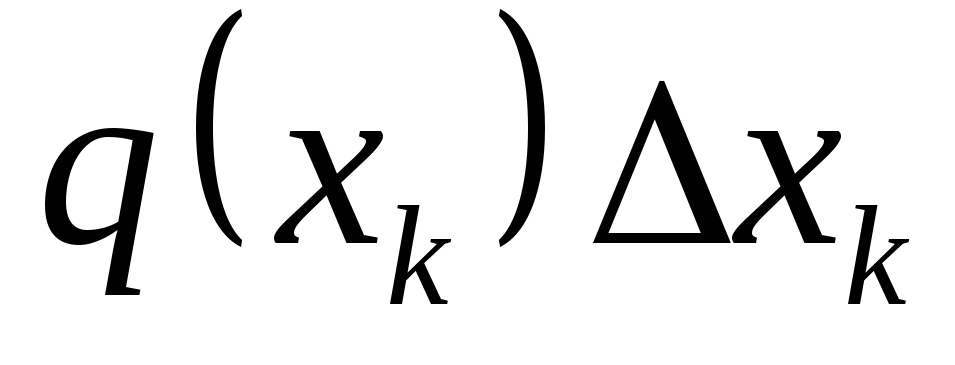, primijenjen u tački 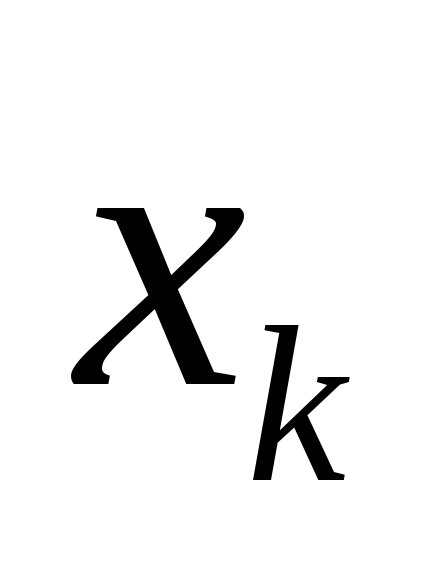(Slika 1.29). Rezultirajući sistem paralelnih sila ima rezultantu jednaku zbroju sila koje djeluju na svaki od segmenata, primijenjenih u centru paralelnih sila.

Jasno je da takva predstava opisuje stvarnu situaciju što je tačnije što je segment manji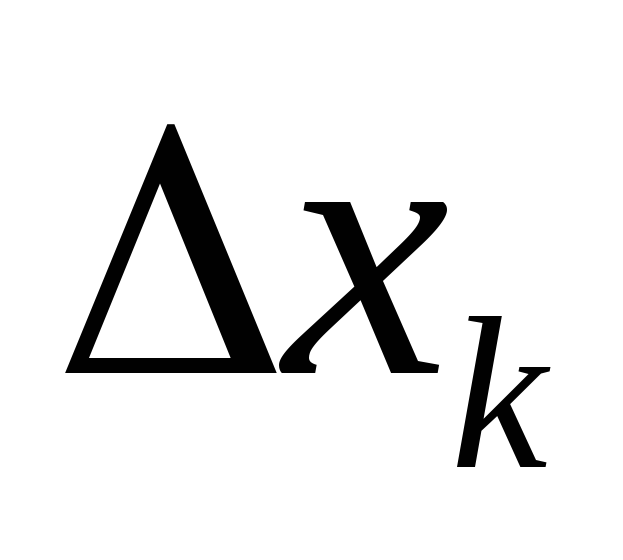

, tj. što više segmenata . Tačan rezultat dobijamo prelaskom do granice na dužini segmenta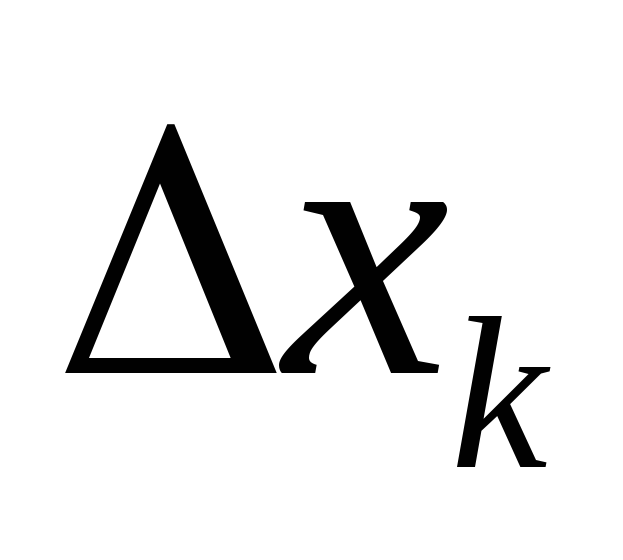

teži nuli. Granica koja proizlazi iz opisanog postupka je integral. Dakle, za modul rezultante dobijamo:

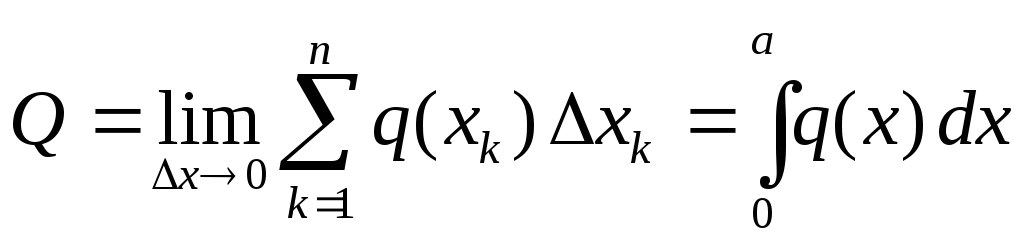
Odrediti koordinate tačke primjenom rezultante koristimo Varignonovu teoremu:

ako sistem sila ima rezultantu, tada je moment rezultante oko bilo kojeg centra (bilo koje ose) jednak zbroju momenata svih sila sistema oko ovog centra (ove ose)

Pisanje ove teoreme za sistem sila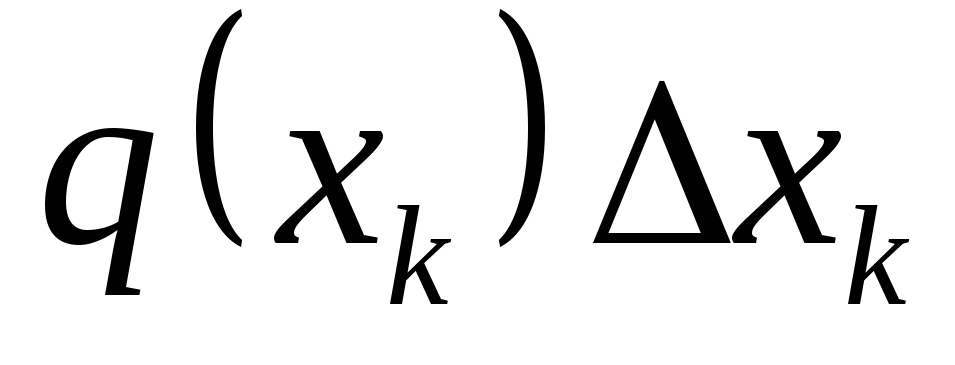

u projekcijama na osi 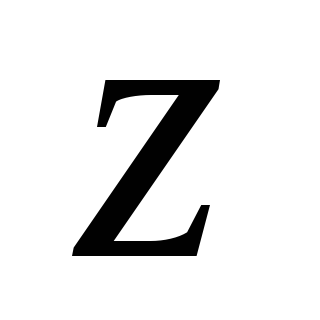i prelazeći do granice sa dužinom segmenata koja teži nuli, dobijamo:

Očigledno, modul rezultante je numerički jednak površini dijagrama raspodijeljenog opterećenja, a točka njegove primjene poklapa se s težištem homogene ploče koja ima oblik dijagrama distribuiranog opterećenja.

Napominjemo dva česta slučaja.

,

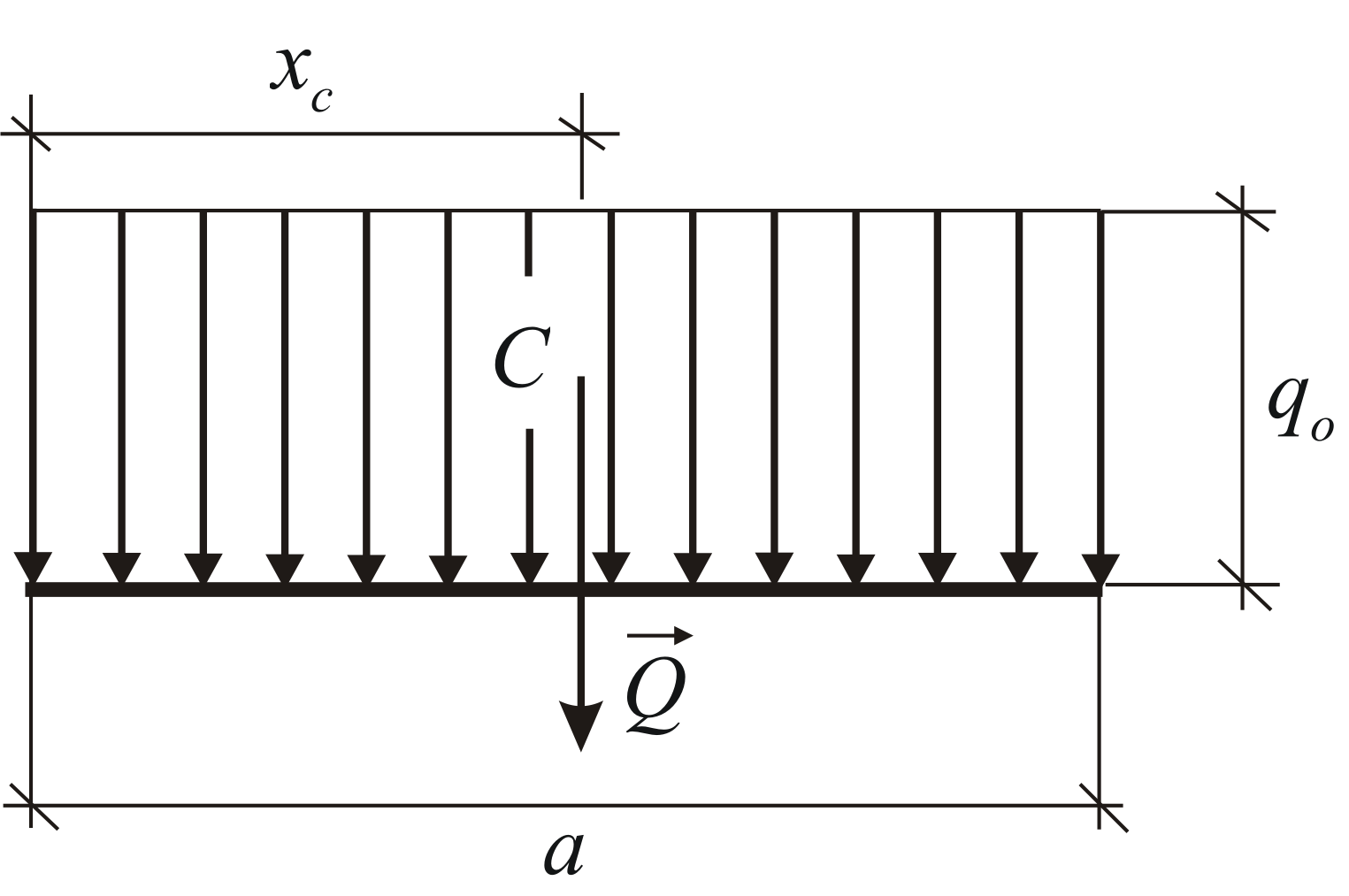
(Sl. 1.30). Rezultantni modul i koordinate njegove tačke primjene određuju se formulama:

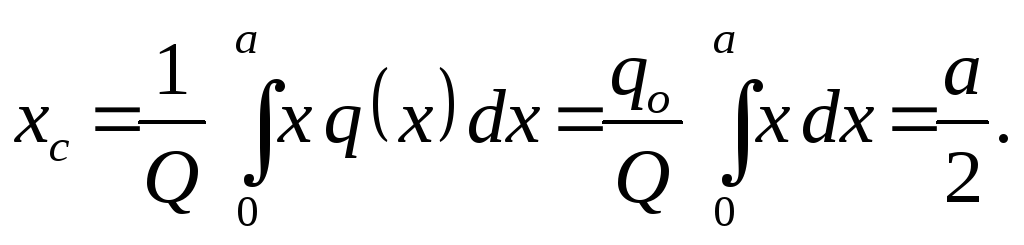
U inženjerskoj praksi takvo je opterećenje prilično uobičajeno. U većini slučajeva, težina i opterećenje vjetrom se mogu smatrati ravnomjerno raspoređenim.

,

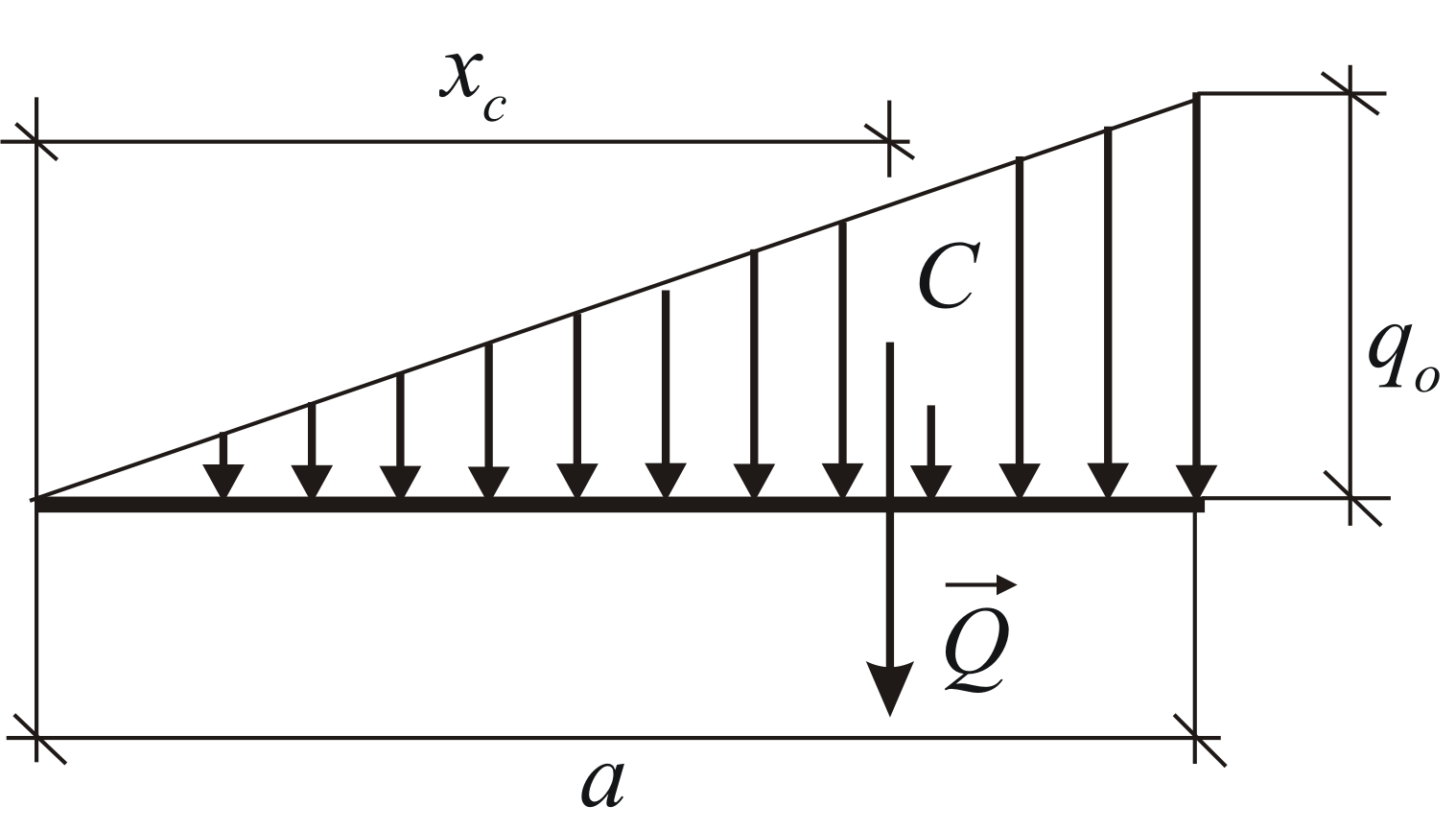
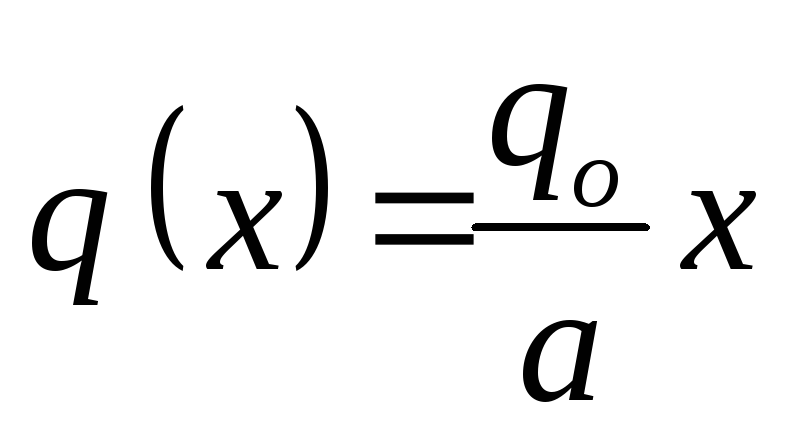(Slika 1.31). U ovom slučaju:

Konkretno, pritisak vode na vertikalni zid je direktno proporcionalan dubini .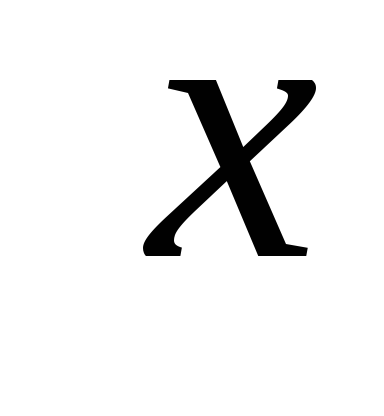

Primjer 1.5

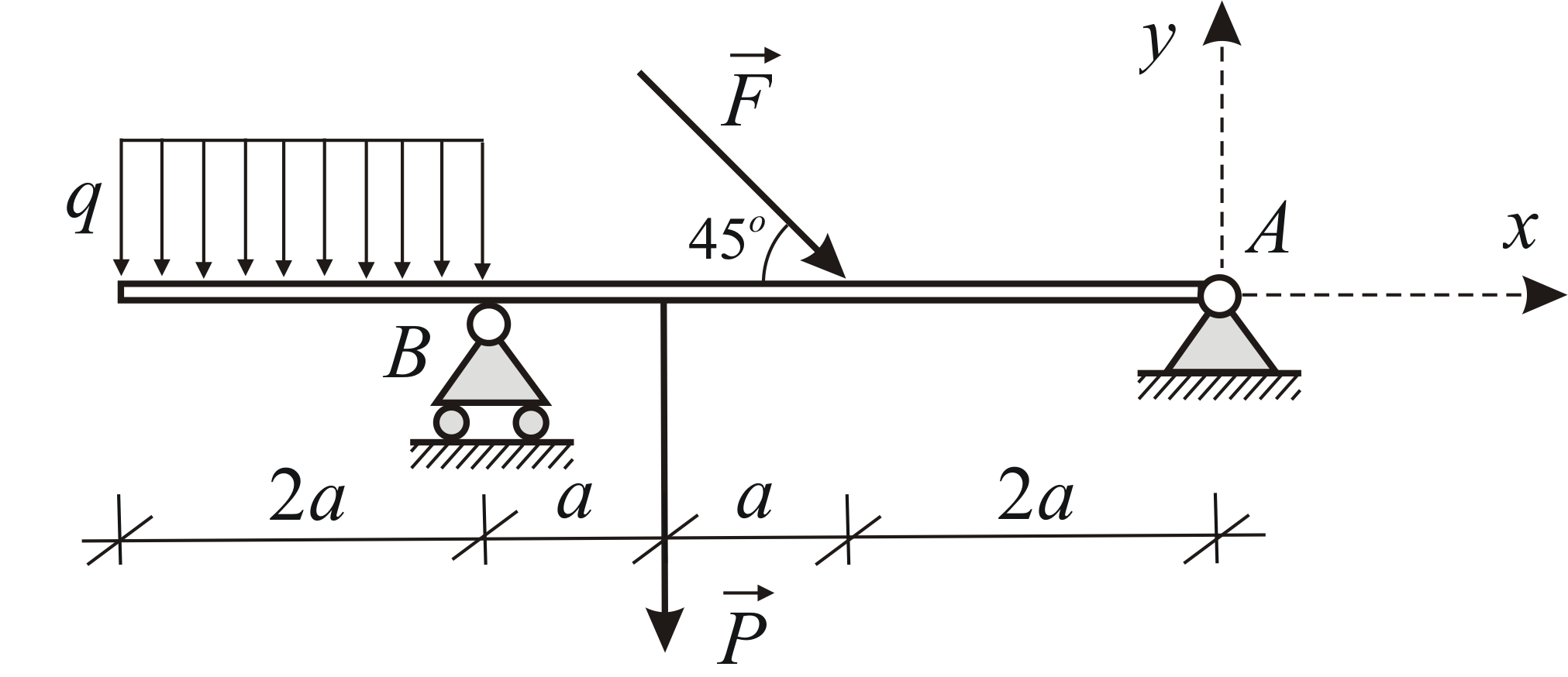
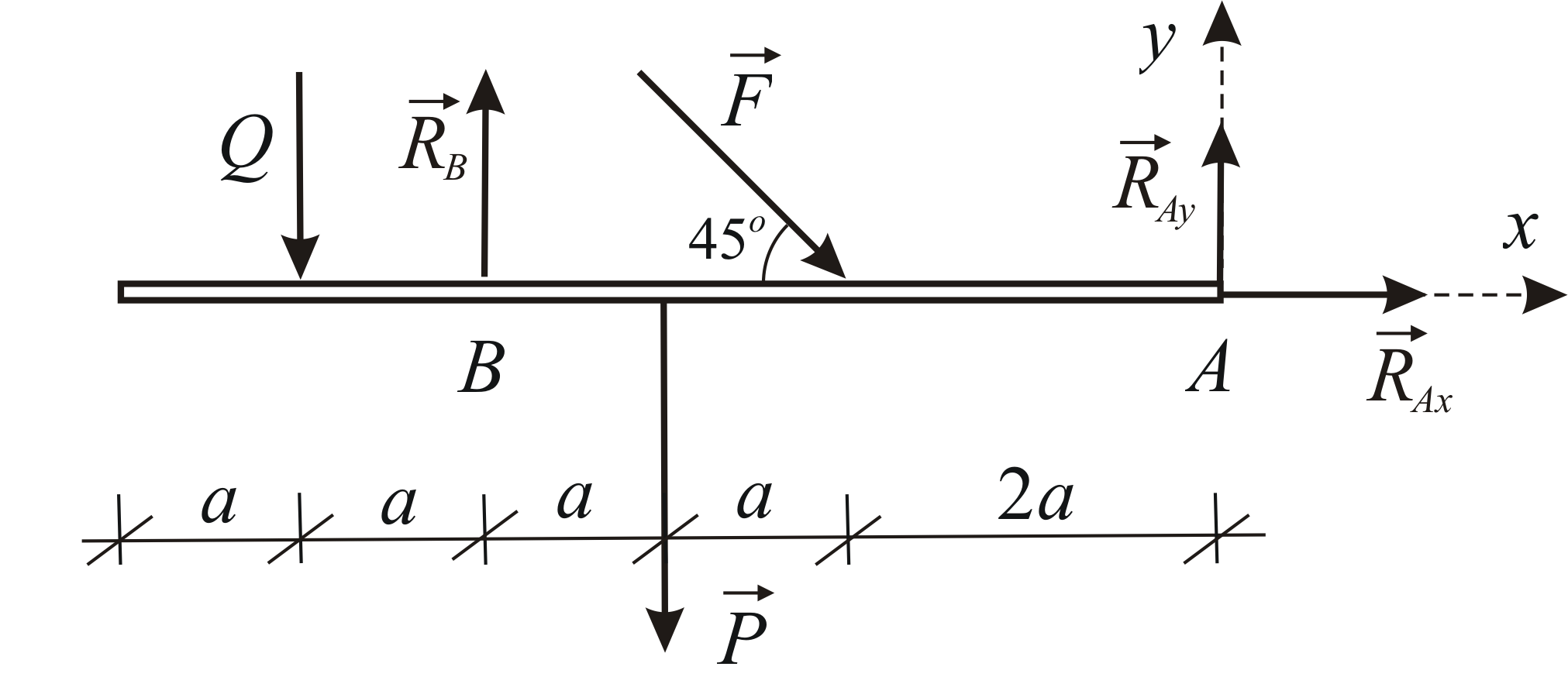
Odredite reakcije nosača i 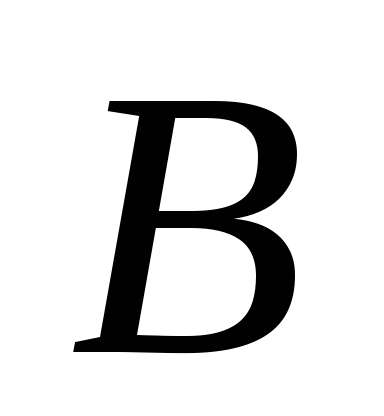greda pod dejstvom dve koncentrisane sile i ravnomerno raspoređenog opterećenja. Dato:

Pronađite rezultantu distribuiranog opterećenja. Rezultantni modul je jednak

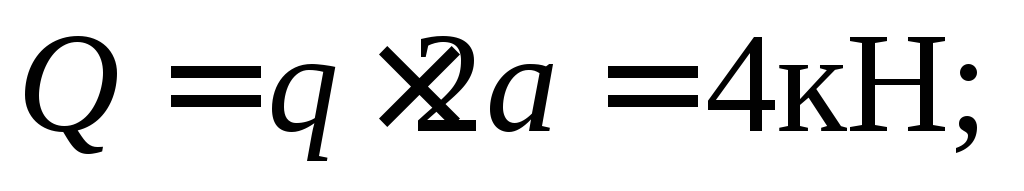
rame snage u odnosu na tačku jednaki

Razmotrite ravnotežu grede. Strujni krug je prikazan na sl. 1.33.

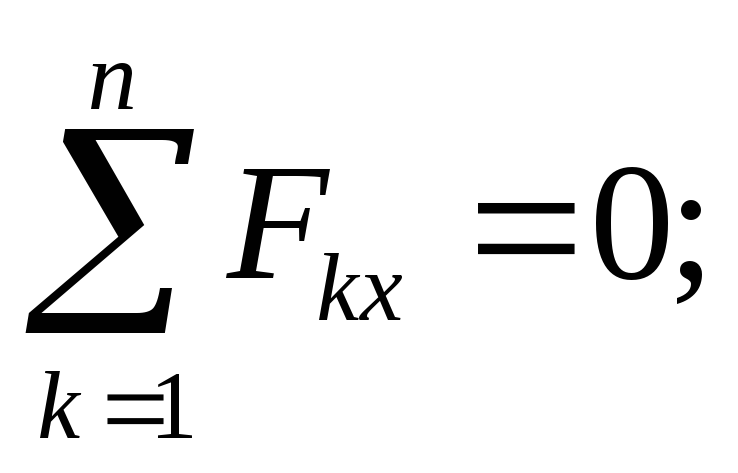
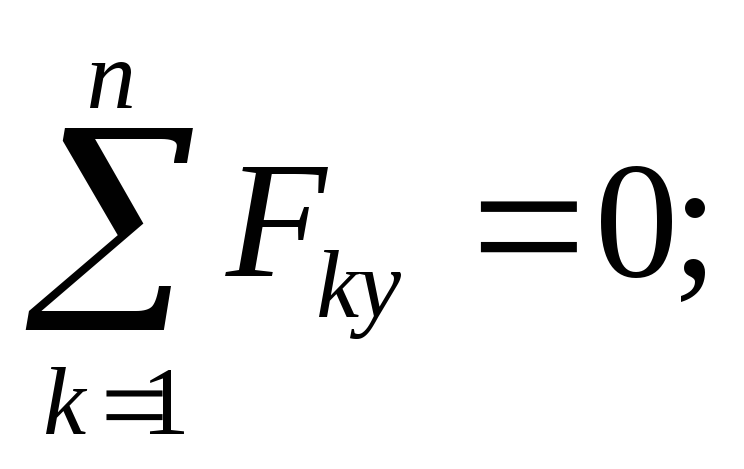
Primjer 1.6

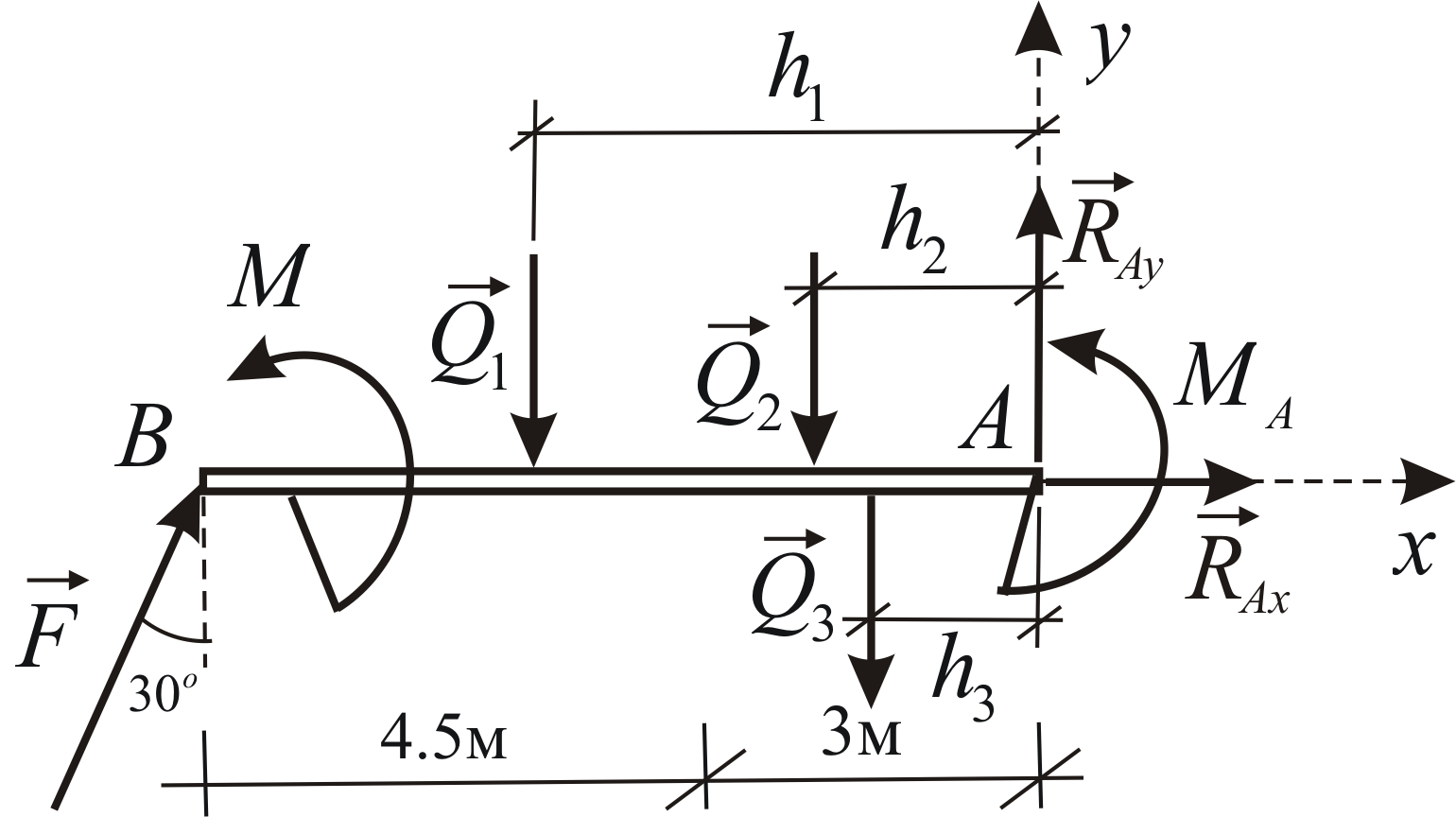
Odredite odziv završetka konzolne grede pod dejstvom koncentrisane sile, para sila i raspoređenog opterećenja (slika 1.34).

Zamijenimo raspoređeno opterećenje sa tri koncentrisane sile. Da bismo to učinili, podijelimo dijagram raspoređenog opterećenja na dva trokuta i pravougaonik. Mi nalazimo

Strujni krug je prikazan na sl. 1.35.

Izračunajte ramena rezultanta u odnosu na osu

Uslovi ravnoteže u slučaju koji se razmatra imaju oblik:

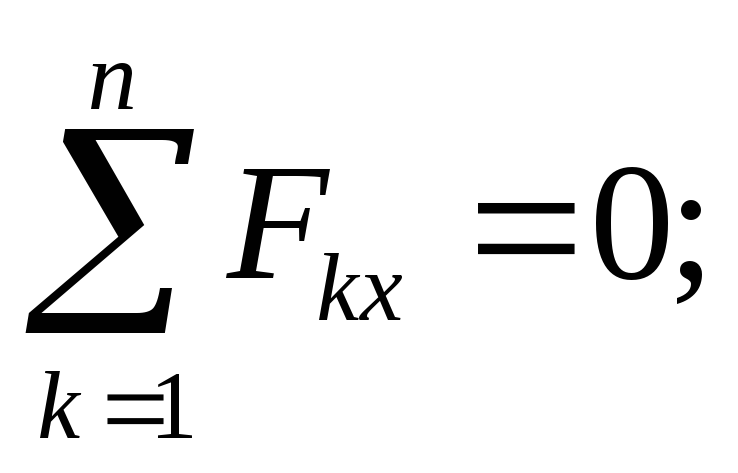
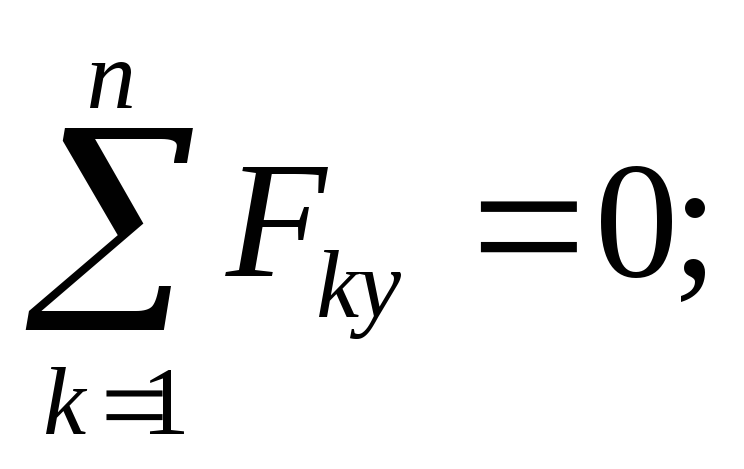
PITANJA ZA SAMOPROVERU:

1. Šta se naziva intenzitetom raspoređenog opterećenja?

2. Kako izračunati modul rezultirajućeg raspoređenog opterećenja?

3. Kako izračunati koordinatu tačke primjene distribuirane rezultante

load?

4. Koji je modul i koja je koordinata tačke primjene ravnomjerno raspoređenog opterećenja?

5. Koji je modul i koja je koordinata tačke primjene linearno raspoređenog opterećenja?

Iz zbirke zadataka I. V. Meshcherskog: 4,28; 4.29; 4.30; 4.33; 4.34.

Iz udžbenika "TEORIJSKA MEHANIKA - teorija i praksa": kompleti SR-2; SR-3.

PRAKTIČNE STUDIJE #4-5

Distribuirana opterećenja

Uticaj na dijelove, konstrukcije, elemente mehanizama može se dati raspoređenim opterećenjima: u ravni sistem intenzitet djelovanja se postavlja duž dužine konstrukcije, u prostornom sistemu - duž područja.

Dimenzija za linearno opterećenje je N / m, za opterećenje raspoređeno po površini - N / m 2, za zapreminu (na primjer, kada se uzme u obzir vlastita težina konstrukcijskih elemenata) - N / m 3.

Na primjer, na slici 1.23, a je prikazan ravnomjerno raspoređen po dužini, mjereno u N/m. Ovo opterećenje se može zamijeniti koncentriranom silom

Q = q∙AB[H],

primijenjen na sredini segmenta AB.

Slika 1.23, b prikazuje ravnomjerno opadajuće (rastuće) opterećenje, koje se može zamijeniti rezultantnom silom

Q = qmax∙AB/2,

primijenjen na tački C, i AC=2/3AB.

U proizvoljnom slučaju, poznavanje funkcije q(x)(Slika 1.23, c), izračunavamo ekvivalentnu silu

Ova sila se primjenjuje u centru gravitacije područja omeđenog iznad grede AB linija q(x).

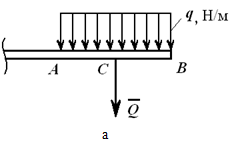
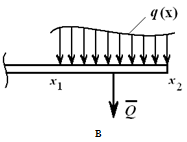
Slika 1.23

Primjer je proračun sila koje razbijaju zidove cilindra sa komprimiranim plinom. Odredimo rezultujuću silu pritiska u sektoru cijevi na intenzitetu q[N/m]; R je polumjer cijevi, 2α– centralni ugao, os Ox- osa simetrije (slika 1.24).

Odaberimo sektorski element sa uglom ∆φ i definiše snagu ∆Q djelujući na ravni lučni element:

∆Q = q ∙ ∆l = q ∙ R ∙ ∆φ. (1.14)

Slika 1.24

Ox bice

∆Q x = q ∙ R ∙ ∆φ∙ cosφ. (1.15)

Zbog simetrije elementa cijevi (sa lukom AB) oko ose Ox projekcija rezultujuće sile na osu Oy:

Q y = 0, tj. Q=Qx, (1.16)

gdje AB je tetiva koja savija krajeve luka.

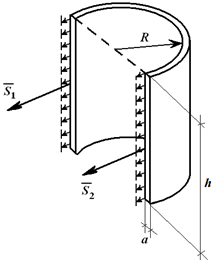
Za cilindrični kontejner visine h i unutrašnji pritisak P zidovi su opterećeni intenzitetom q = p [N/m, 2 ]. Ako je cilindar izrezan u prečniku (slika 1.25), onda je jednak F = q ∙ d ∙ h (d– unutrašnji prečnik) ili

F = p ∙ 2R ∙ h.

Cepanje balona prečnikom napora:

S 1 = S 2 = S;
2S=F;
S = p∙h∙R. (1.18)

U inženjerskim proračunima se često susreću opterećenja raspoređena duž date površine prema jednom ili drugom zakonu. Razmotrimo neke od najjednostavnijih primjera raspoređenih sila koje leže u istoj ravni.

Ravni sistem raspoređenih sila karakteriše njegov intenzitet q, odnosno vrijednost sile po jedinici dužine opterećenog segmenta. Intenzitet se mjeri u njutnima podijeljeno metrima.

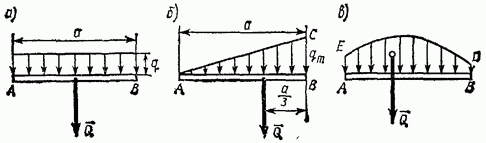
1) Sile ravnomerno raspoređene duž pravolinijskog segmenta (slika 69, a). Za takav sistem sila, intenzitet q ima konstantnu vrijednost. U statičkim proračunima, ovaj sistem sila može se zamijeniti rezultantom

Modulo

Na sredinu segmenta AB primjenjuje se sila Q.

2) Sile raspoređene duž pravolinijskog segmenta prema linearnom zakonu (slika 69, b). Primjer takvog opterećenja mogu biti sile pritiska vode na branu, koje imaju najveća vrijednost na dnu i pada na nulu na površini vode. Za ove sile, intenzitet q je promjenjiva vrijednost koja raste od nule do maksimalne vrijednosti.Rezultanta Q takvih sila određuje se slično kao rezultanta sila gravitacije koje djeluju na jednoličnu trokutnu ploču ABC. Budući da je težina homogene ploče proporcionalna njenoj površini, onda po modulu,

Na rastojanju od stranice BC trougla ABC deluje sila Q (vidi § 35, tačka 2).

3) Sile raspoređene duž pravolinijskog segmenta prema proizvoljnom zakonu (slika 69, c). Rezultantna Q takvih sila, po analogiji sa silom gravitacije, po apsolutnoj je vrijednosti jednaka površini figure ABDE, mjerenoj na odgovarajućoj skali, i prolazi kroz težište ovog područja ( pitanje određivanja centara gravitacije oblasti će se razmatrati u § 33).

4) Sile ravnomerno raspoređene duž luka kružnice (Sl. 70). Primjer takvih sila su sile hidrostatskog pritiska na bočne stijenke cilindrične posude.

Neka je polumjer luka , gdje je os simetrije duž koje usmjeravamo osu.Sistem konvergentnih sila koje djeluju na luk ima rezultantu Q, usmjerenu duž ose zbog simetrije, dok

Da bismo odredili vrijednost Q, izaberemo element na luku čiji je položaj određen uglom i dužinom.Sila koja djeluje na ovaj element je brojčano jednaka i projekcija ove sile na os će biti Tada

Ali sa Sl. 70 može se vidjeti da Stoga, od tada

gdje je dužina tetive koja savija luk AB; q - intenzitet.

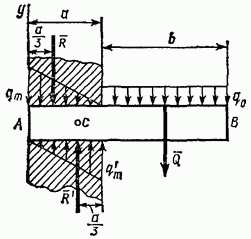
Zadatak 27. Na konzolnu gredu A B, čije su dimenzije prikazane na crtežu (Sl. 71), djeluje ravnomjerno raspoređeno opterećenje intenziteta.

Rješenje. Mi zamenjujemo raspoređene snage njihove rezultante Q, R i R, gdje su prema formulama (35) i (36)

i sastaviti uslove ravnoteže (33) za paralelne sile koje deluju na gredu

Zamjenjujući ovdje umjesto Q, R i R njihove vrijednosti i rješavajući rezultirajuće jednadžbe, konačno nalazimo

Na primjer, ako dobijemo i ako

Zadatak 28. Cilindrični cilindar čija je visina H, a unutrašnji prečnik d ispunjen je gasom pod pritiskom.Debljina cilindričnih zidova cilindra je a. Odredite vlačna naprezanja koja doživljavaju ovi zidovi u smjerovima: 1) uzdužnom i 2) poprečnom (napon je jednak omjeru vlačne sile i površine poprečnog presjeka), smatrajući ga malim.

Rješenje. 1) Razrežemo cilindar ravninom okomitom na njegovu osu na dva dijela i razmotrimo ravnotežu jednog od njih (sl.

72a). Na njega u smjeru ose cilindra djeluju sila pritiska na dno i sile raspoređene po površini poprečnog presjeka (djelovanje odbačene polovine), čija je rezultanta označena sa Q. U ravnoteži

Udaljenost između koncentriranih opterećenja je ista, dok je udaljenost od početka raspona do prvog koncentriranog opterećenja jednaka udaljenosti između koncentriranih opterećenja. U ovom slučaju koncentrirana opterećenja padaju i na početku i na kraju raspona, ali u ovom slučaju samo uzrokuju povećanje reakcija podrške, ekstremno koncentrisana opterećenja ne utječu na vrijednost momenata savijanja i progiba, te stoga u proračunima nosivost strukture se ne uzimaju u obzir. Razmotrite to na primjeru podnih greda na bazi nadvratnika. Zidanje od cigle, koji može biti između nadvratnika i podne grede, a istovremeno stvarati jednoliko raspoređeno opterećenje, nije prikazan radi lakše percepcije.

Slika 1. Dovođenje koncentrisanih opterećenja do ekvivalentnog ravnomjerno raspoređenog opterećenja.

Kao što se može vidjeti na slici 1, određujući moment je moment savijanja, koji se koristi u proračunima čvrstoće konstrukcija. Dakle, da bi ravnomjerno raspoređeno opterećenje proizvelo isti moment savijanja kao koncentrirano opterećenje, mora se pomnožiti s odgovarajućim prijelaznim faktorom (faktor ekvivalencije). I ovaj koeficijent se određuje iz uslova jednakosti momenata. Mislim da slika 1 to vrlo dobro ilustruje. Pa ipak, analizom dobijenih zavisnosti moguće je izvesti opštu formulu za određivanje prelaznog koeficijenta. Dakle, ako je broj primijenjenih koncentrisanih opterećenja neparan, tj. jedno od koncentriranih opterećenja nužno pada na sredinu raspona, a zatim da biste odredili koeficijent ekvivalencije, možete koristiti formulu:

γ = n/(n - 1) (305.1.1)

gdje je n broj raspona između koncentriranih opterećenja.

q ekvivalent = γ(n-1)Q/l (305.1.2)

gdje je (n-1) broj koncentrisanih opterećenja.

Međutim, ponekad je prikladnije napraviti proračune na osnovu broja koncentriranih opterećenja. Ako je ova količina izražena varijablom m, onda

γ = (m+1)/m (305.1.3)

U ovom slučaju, ekvivalentno ravnomjerno raspoređeno opterećenje će biti jednako:

q ekvivalent = γmQ/l (305.1.4)

Kada je broj koncentrisanih opterećenja paran, tj. nijedno od koncentrisanih opterećenja ne pada na sredinu raspona, tada se vrijednost koeficijenta može uzeti kao za sljedeću neparnu vrijednost broja koncentrisanih opterećenja. Općenito, ovisno o specificiranim uvjetima opterećenja, mogu se uzeti sljedeći faktori konverzije:

γ = 2- ako samo jedno koncentrisano opterećenje u sredini nadvratnika padne na konstrukciju koja se razmatra, na primjer, gredu.

γ = 1,33- za gredu na koju djeluju 2 ili 3 koncentrisana opterećenja;

γ = 1,2- za gredu na koju djeluju 4 ili 5 koncentrisanih opterećenja;

γ = 1,142- za gredu na koju djeluje 6 ili 7 koncentriranih opterećenja;

γ = 1,11- za gredu na koju djeluje 8 ili 9 koncentriranih opterećenja.

Opcija 2

Udaljenost između koncentriranih opterećenja je ista, dok je udaljenost od početka raspona do prvog koncentriranog opterećenja jednaka polovini udaljenosti između koncentriranih opterećenja. U ovom slučaju koncentrirana opterećenja ne padaju na početak i kraj raspona.

Slika 2. Vrijednosti prijelaznih koeficijenata za 2. varijantu primjene koncentriranih opterećenja.

Kao što se može vidjeti sa slike 2, sa ovom opcijom učitavanja vrijednost koeficijenta prijelaza bit će znatno manja. Tako se, na primjer, s parnim brojem koncentriranih opterećenja, prijelazni koeficijent općenito može uzeti jednakim jedinici. Uz neparan broj koncentriranih opterećenja, formula se može koristiti za određivanje faktora ekvivalencije:

γ = (m+7)/(m+6) (305.2.1)

gdje je m broj koncentrisanih opterećenja.

U ovom slučaju, ekvivalentno ravnomjerno raspoređeno opterećenje i dalje će biti jednako:

q ekvivalent = γmQ/l (305.1.4)

Općenito, ovisno o specificiranim uvjetima opterećenja, mogu se uzeti sljedeći faktori konverzije:

γ = 2- ako samo jedno koncentrisano opterećenje u sredini nadvratnika padne na konstrukciju koja se razmatra, na primjer, i da li podne grede padaju na početak ili kraj raspona ili se nalaze proizvoljno udaljene od početka i kraja raspona, u ovom slučaju to nije bitno. A ovo je važno za određivanje koncentriranog opterećenja.

γ = 1- ako na predmetnu konstrukciju djeluje paran broj opterećenja.

γ = 1,11- za gredu na koju djeluju 3 koncentrisana opterećenja;

γ = 1,091- za gredu na koju djeluje 5 koncentrisanih opterećenja;

γ = 1,076- za gredu na koju djeluje 7 koncentrisanih opterećenja;

γ = 1,067- za gredu na koju djeluje 9 koncentriranih opterećenja.

Uprkos nekim lukavim definicijama, koeficijenti ekvivalencije su vrlo jednostavni i pogodni. Budući da je u proračunima vrlo često poznato raspoređeno opterećenje koje djeluje na kvadratni ili tekući metar, da se raspoređeno opterećenje ne bi pretvorilo prvo u koncentrisano, a zatim opet u ekvivalentno raspoređeno, dovoljno je jednostavno pomnožiti vrijednost raspoređeno opterećenje odgovarajućim koeficijentom. Na primjer, na pod će djelovati normativno raspoređeno opterećenje od 400 kg / m 2, dok će vlastita težina poda biti još 300 kg / m 2. Tada bi s dužinom podne grede od 6 m na nadvratnik moglo djelovati ravnomjerno raspoređeno opterećenje q = 6(400 + 300)/2 = 2100 kg/m. A onda, ako postoji samo jedna podna greda u sredini raspona, onda je γ = 2, i

q ekvivalent = γq = 2q (305.2.2)

Ako nijedan od gornja dva uvjeta nije ispunjen, tada je nemoguće koristiti prijelazne koeficijente u njihovom čistom obliku, potrebno je dodati još par dodatnih koeficijenata koji uzimaju u obzir udaljenost do greda koje ne padaju na početku i kraja raspona nadvratnika, kao i moguća asimetrija primjene koncentrisanih opterećenja. U principu, moguće je izvesti takve koeficijente, međutim, u svakom slučaju, oni će se smanjiti u svim slučajevima, ako uzmemo u obzir 1. opciju opterećenja i u 50% slučajeva, ako uzmemo u obzir 2. opciju opterećenja, tj. vrijednosti takvih koeficijenata će biti< 1. А потому для упрощения расчетов, а заодно и для большего запаса по прочности рассчитываемой конструкции вполне хватит коэффициентов, приведенных при первых двух вариантах загружения.

Distribuirana opterećenja

Uticaj na dijelove, konstrukcije, elemente mehanizama može se odrediti raspoređenim opterećenjima: u ravnom sistemu intenzitet djelovanja je postavljen po dužini konstrukcije, u prostornom sistemu - po površini.

Dimenzija za linearno opterećenje je N / m, za opterećenje raspoređeno po površini - N / m 2, za zapreminu (na primjer, kada se uzme u obzir vlastita težina konstrukcijskih elemenata) - N / m 3.

Na primjer, na slici 1.23, a je prikazan ravnomjerno raspoređen po dužini, mjereno u N/m. Ovo opterećenje se može zamijeniti koncentriranom silom

Q = q∙AB[H],

primijenjen na sredini segmenta AB.

Slika 1.23, b prikazuje ravnomjerno opadajuće (rastuće) opterećenje, koje se može zamijeniti rezultantnom silom

Q = qmax∙AB/2,

primijenjen na tački C, i AC=2/3AB.

U proizvoljnom slučaju, poznavanje funkcije q(x)(Slika 1.23, c), izračunavamo ekvivalentnu silu

Ova sila se primjenjuje u centru gravitacije područja omeđenog iznad grede AB linija q(x).

Slika 1.23

Primjer je proračun sila koje razbijaju zidove cilindra sa komprimiranim plinom. Odredimo rezultujuću silu pritiska u sektoru cijevi na intenzitetu q[N/m]; R je polumjer cijevi, 2α– centralni ugao, os Ox- osa simetrije (slika 1.24).

Odaberimo sektorski element sa uglom ∆φ i definiše snagu ∆Q djelujući na ravni lučni element:

∆Q = q ∙ ∆l = q ∙ R ∙ ∆φ. (1.14)

Slika 1.24

Ox bice

∆Q x = q ∙ R ∙ ∆φ∙ cosφ. (1.15)

Zbog simetrije elementa cijevi (sa lukom AB) oko ose Ox projekcija rezultujuće sile na osu Oy:

Q y = 0, tj. Q=Qx, (1.16)

gdje AB je tetiva koja savija krajeve luka.

Za cilindrični kontejner visine h i unutrašnji pritisak P zidovi su opterećeni intenzitetom q = p [N/m, 2 ]. Ako je cilindar izrezan u prečniku (slika 1.25), onda je jednak F = q ∙ d ∙ h (d– unutrašnji prečnik) ili

F = p ∙ 2R ∙ h.

Cepanje balona prečnikom napora:

S 1 = S 2 = S;
2S=F;
S = p∙h∙R. (1.18)