Nerovnomerne rozložené zaťaženie. Rozložené zaťaženie
Povrchové a objemové sily predstavujú zaťaženie rozložené na určitý povrch alebo objem. Takéto zaťaženie je dané intenzitou, čo je sila na jednotku nejakého objemu, alebo nejakej plochy, alebo nejakej dĺžky.
Osobitné miesto pri riešení množstva prakticky zaujímavých problémov zaujíma prípad plošne rozloženého zaťaženia aplikovaného pozdĺž normály na určitý nosník. Ak nasmerujete os pozdĺž lúča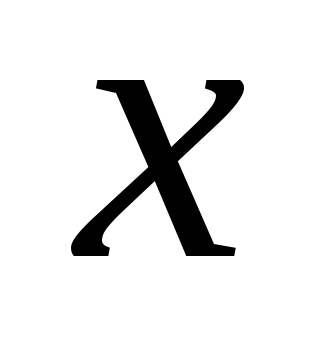 
, potom bude intenzita funkciou súradnice 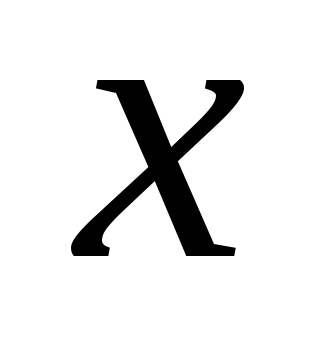a meria sa v N/m. Intenzita je sila na jednotku dĺžky.
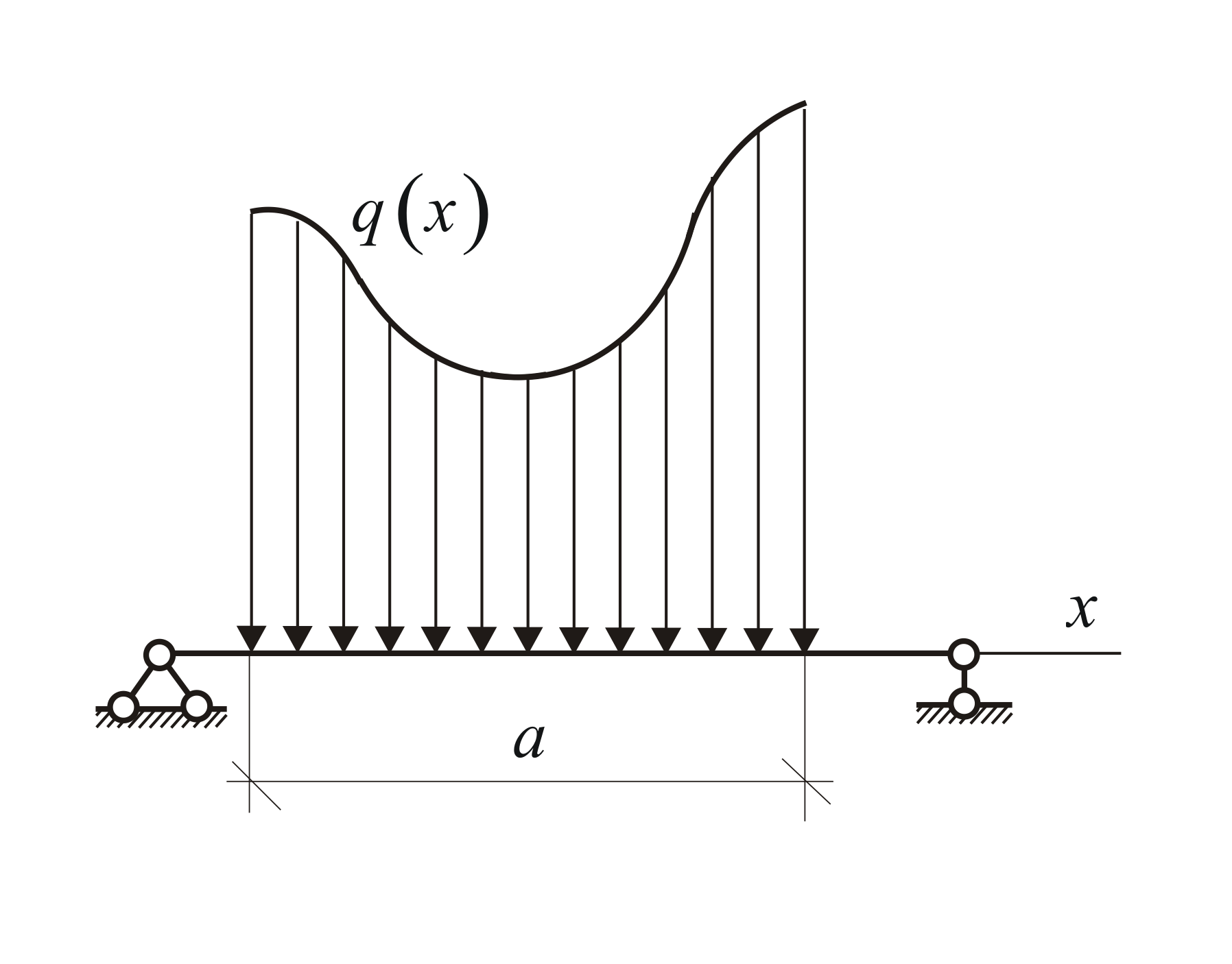
Plochý útvar ohraničený nosníkom a grafom intenzity zaťaženia sa nazýva diagram rozloženého zaťaženia (obr. 1.28). Ak z povahy riešeného problému možno ignorovať deformácie, t.j. Keďže teleso možno považovať za absolútne tuhé, rozložené zaťaženie môže (a malo by) byť nahradené výslednicou.
|
|
|
|
Rozdelíme lúč na 
dĺžkové segmenty 
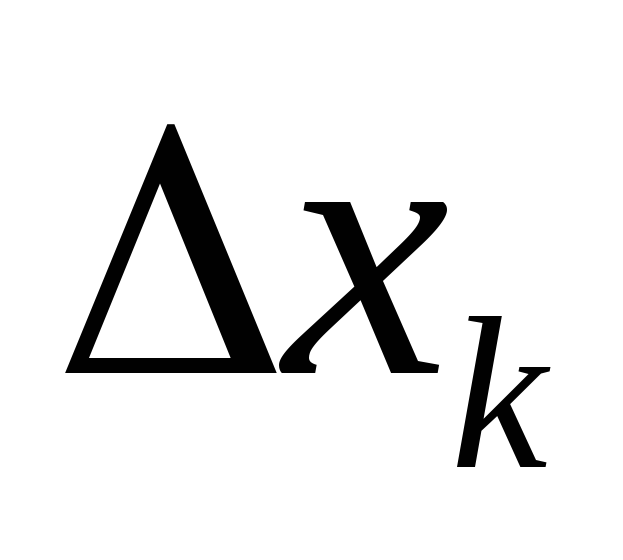, na každom z nich predpokladáme, že intenzita je konštantná a rovná sa 
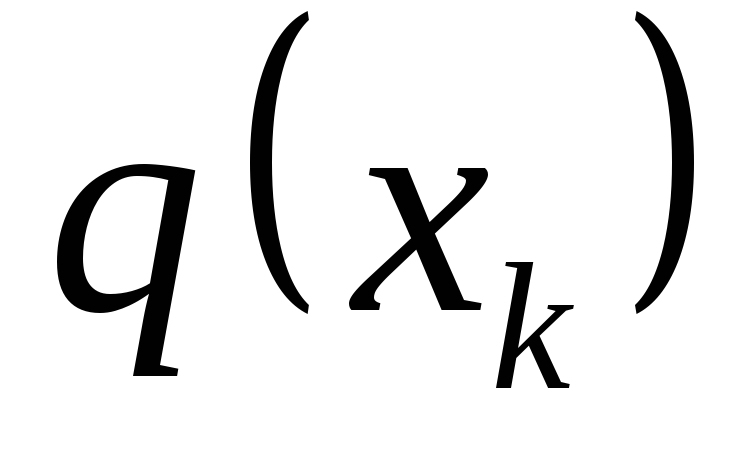, kde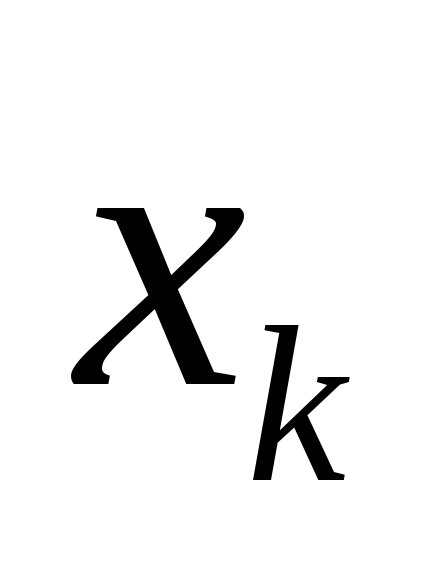 
- súradnica segmentu 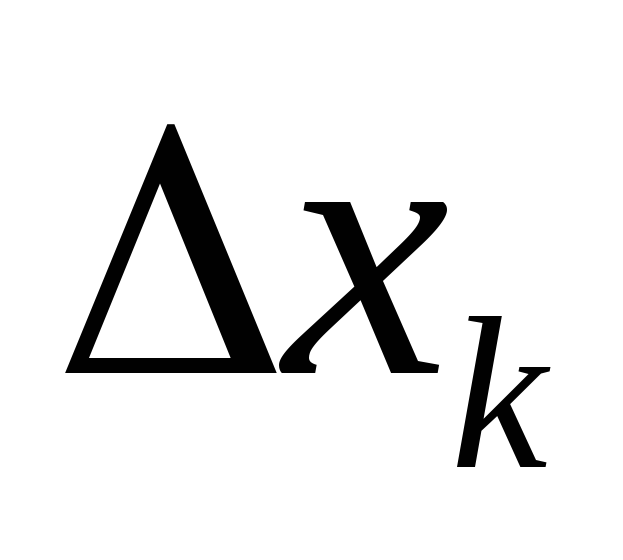. V tomto prípade je krivka intenzity nahradená prerušovanou čiarou a záťažou na segment 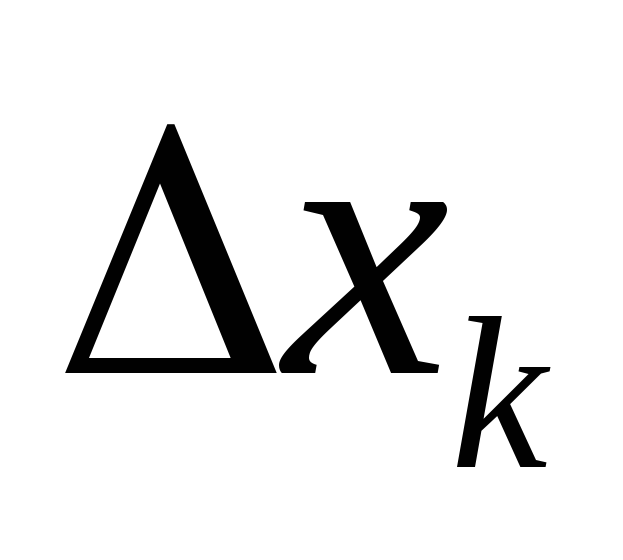, je nahradená sústredenou silou 
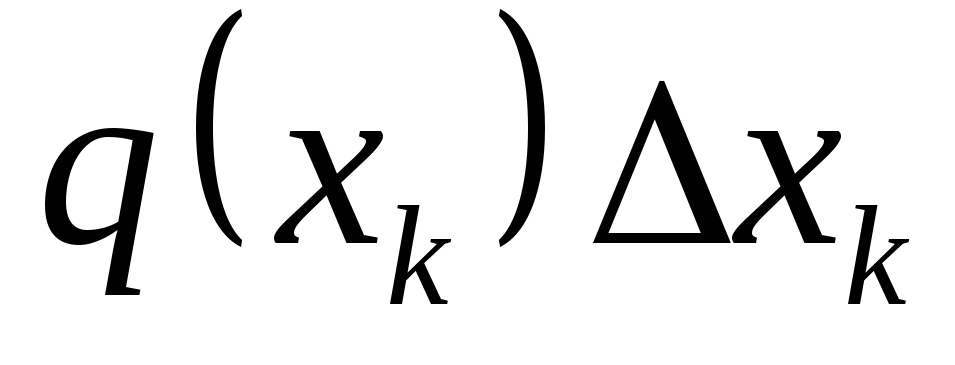, aplikovaný v bode 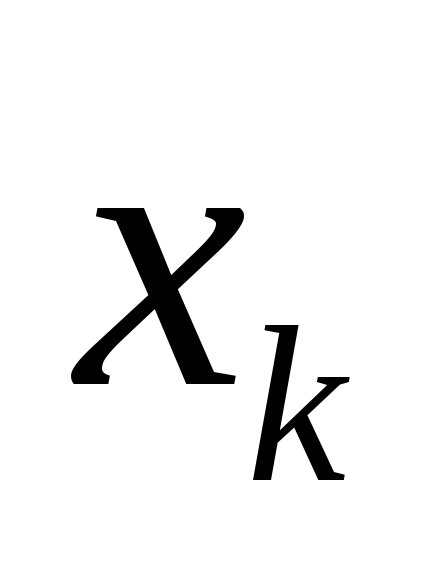(Obrázok 1.29). Výsledný systém rovnobežných síl má výslednicu rovnajúcu sa súčtu síl pôsobiacich na každý zo segmentov aplikovaných v strede rovnobežných síl.
Je zrejmé, že takéto zobrazenie popisuje reálny stav tým presnejšie, čím je segment menší 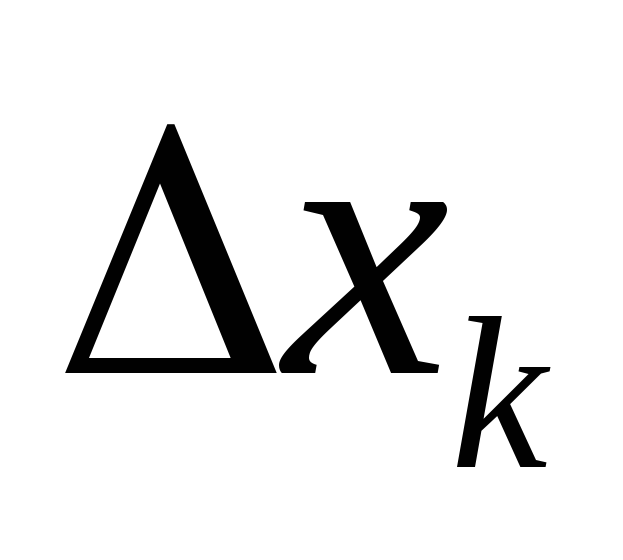, t.j. čím viac segmentov . Presný výsledok získame prechodom na limit na dĺžke segmentu 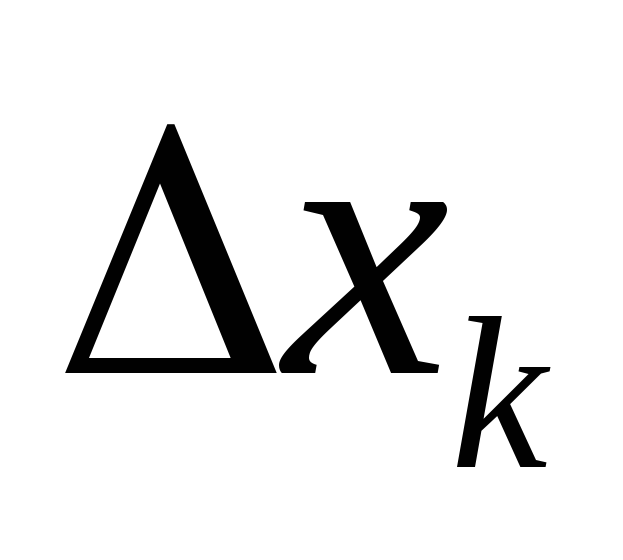sklon k nule. Limit vyplývajúci z opísaného postupu je integrál. Pre modul výslednice teda dostaneme:
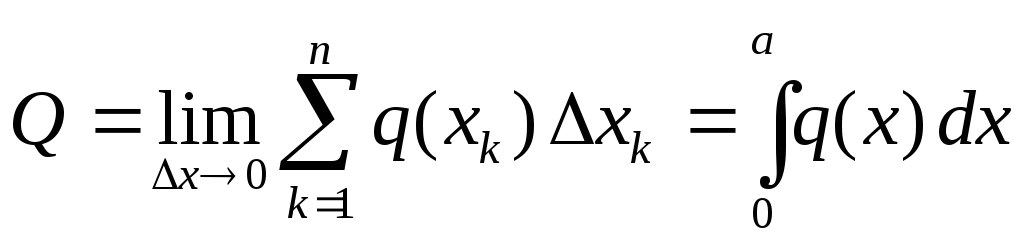
Na určenie súradníc bodu 
pri aplikácii výslednice použijeme Varignonovu vetu:
ak má sústava síl výslednicu, tak moment výslednice okolo ľubovoľného stredu (ľubovoľnej osi) sa rovná súčtu momentov všetkých síl sústavy okolo tohto stredu (tejto osi)
Písanie tejto vety pre sústavu síl 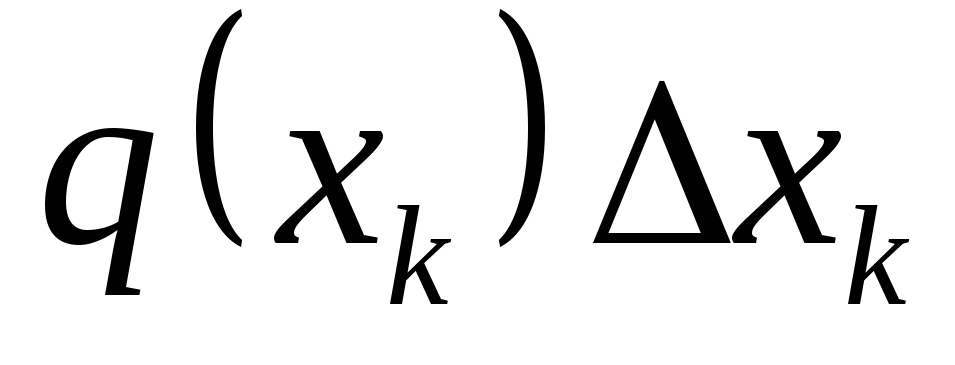v projekciách na os 
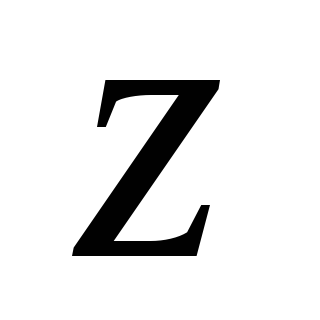a prechodom na limit s dĺžkou segmentov smerujúcou k nule dostaneme:
Je zrejmé, že modul výslednice sa číselne rovná ploche diagramu rozloženého zaťaženia a bod jeho aplikácie sa zhoduje s ťažiskom homogénnej dosky vo forme diagramu rozloženého zaťaženia.
Zaznamenali sme dva často sa vyskytujúce prípady.
,
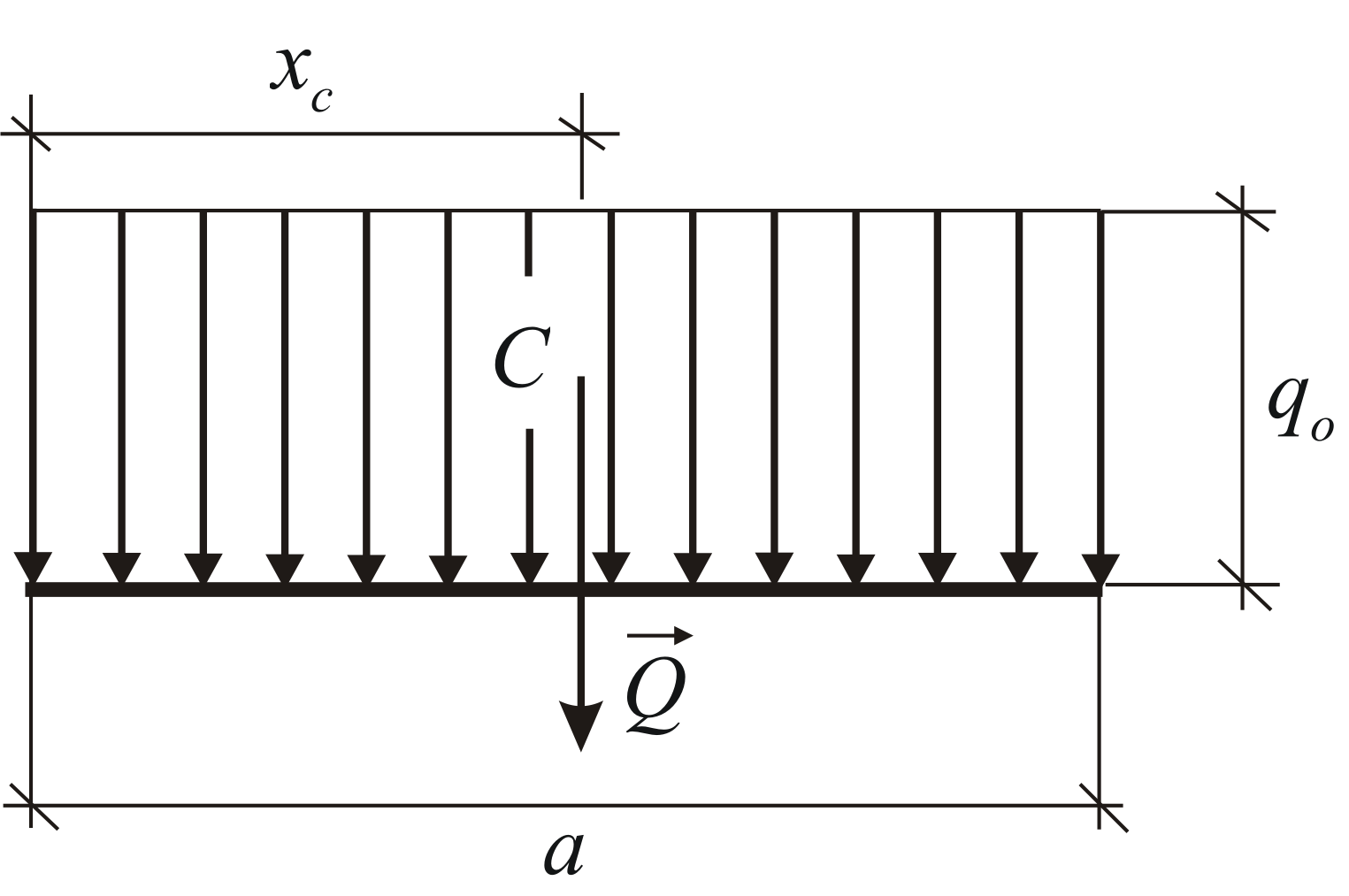
(obr. 1.30). Výsledný modul a súradnice jeho aplikačného bodu sú určené vzorcami:
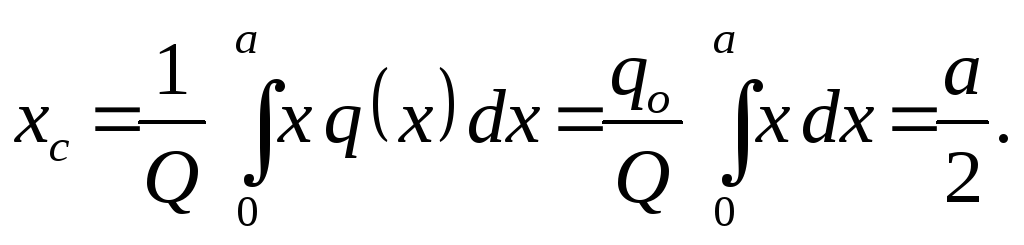
V strojárskej praxi je takéto zaťaženie celkom bežné. Vo väčšine prípadov možno hmotnosť a zaťaženie vetrom považovať za rovnomerne rozložené.
|
|
|
|
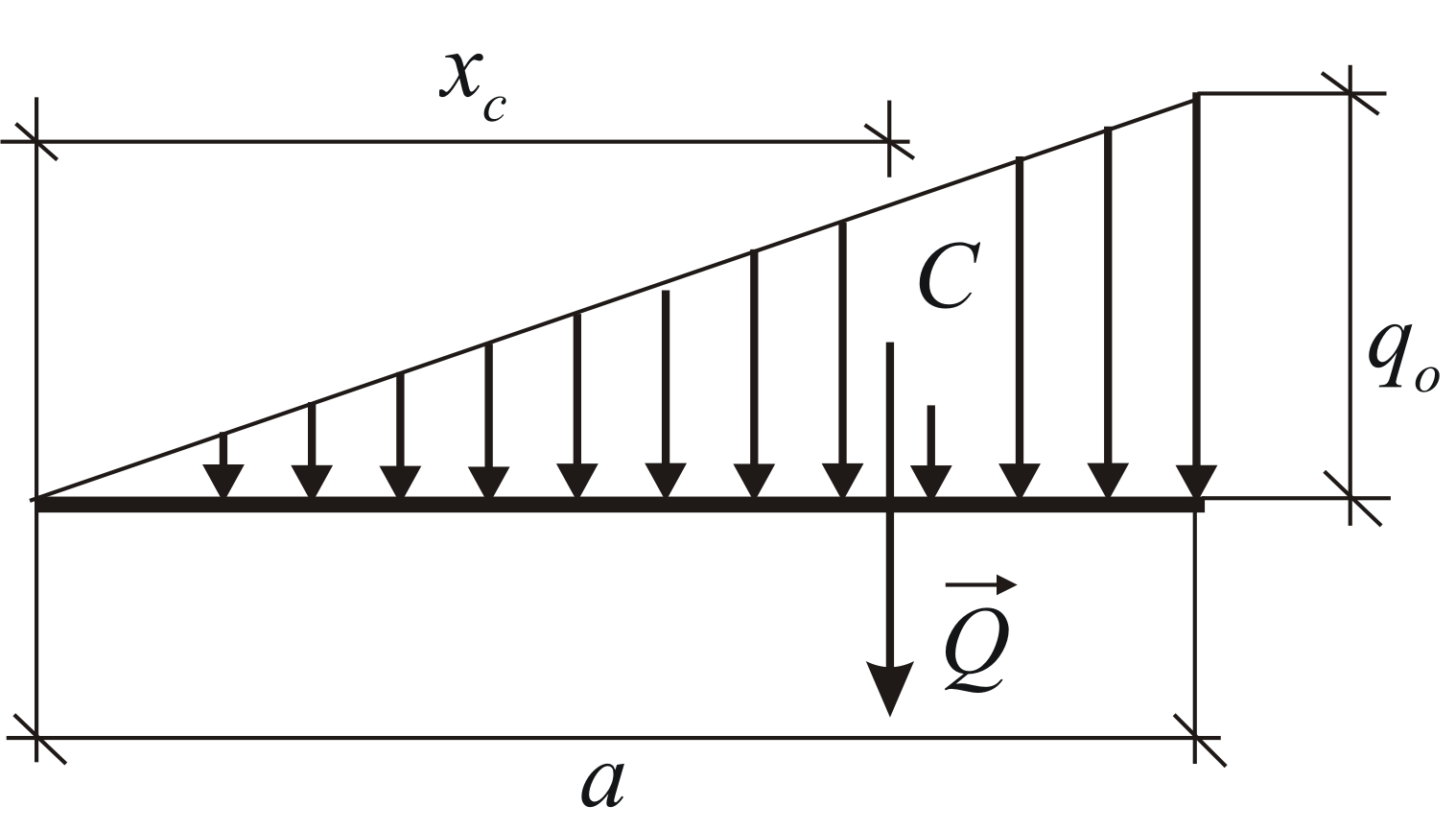
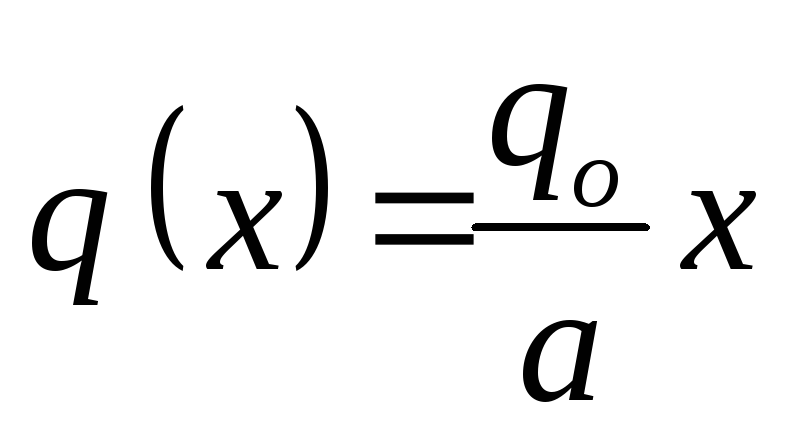(Obrázok 1.31). V tomto prípade:
Najmä tlak vody na zvislú stenu je priamo úmerný hĺbke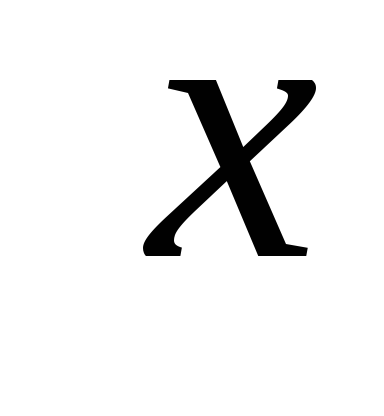 
.
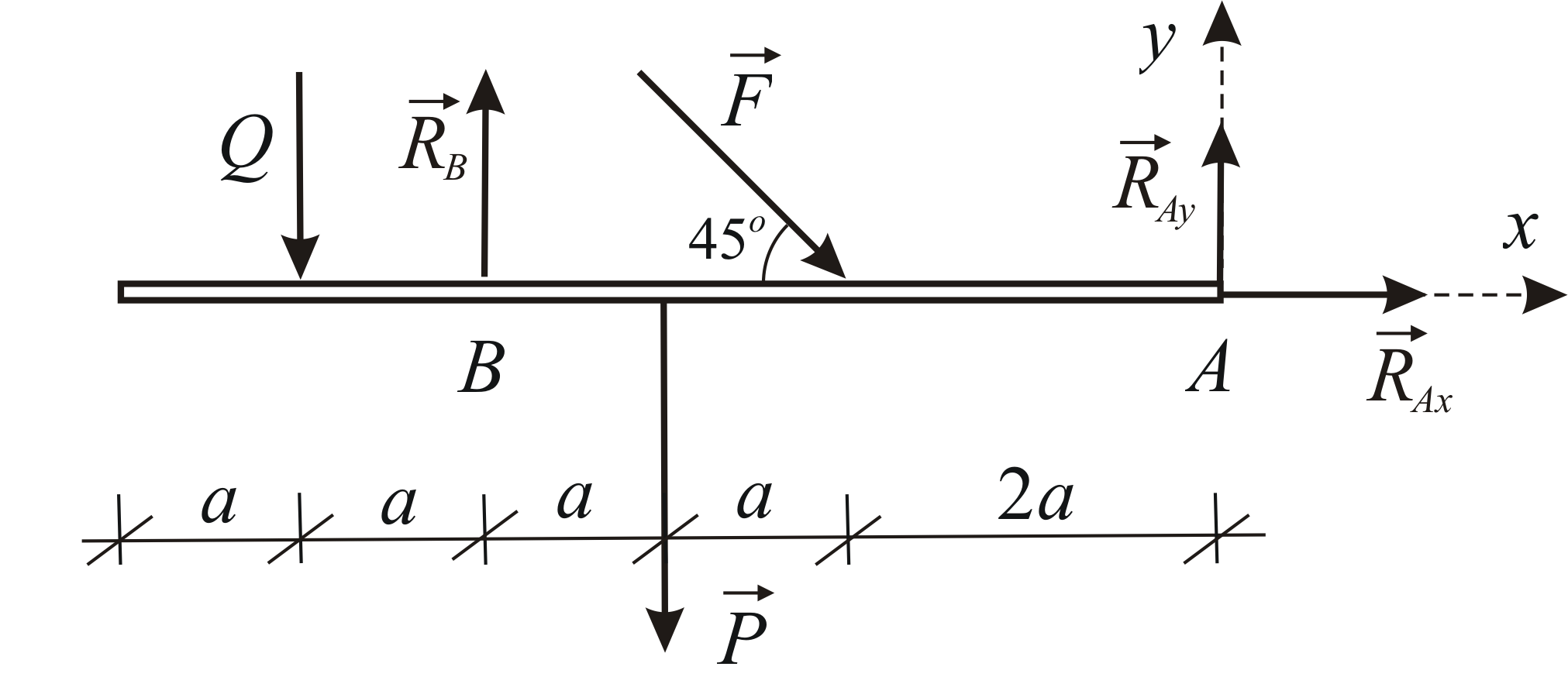
Príklad 1.5
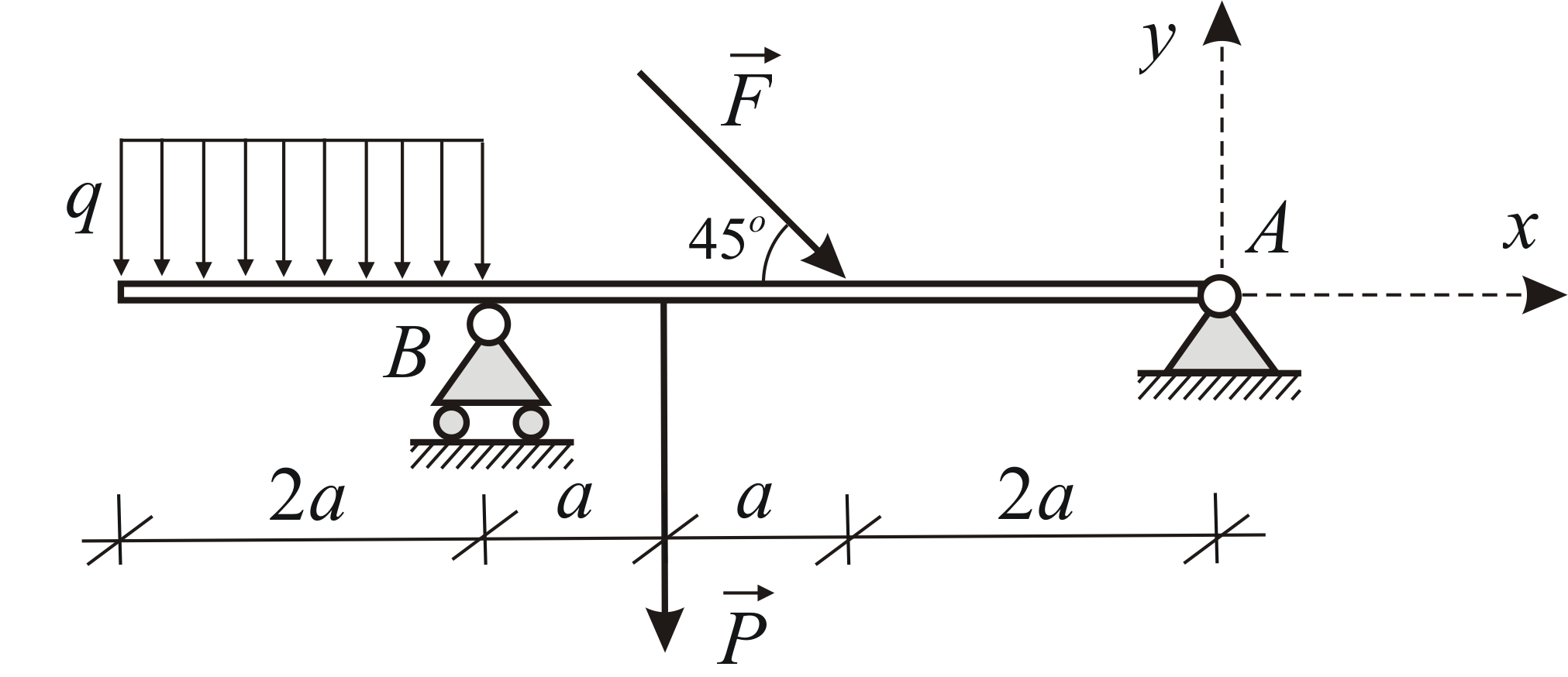
Určte reakcie podpier 
a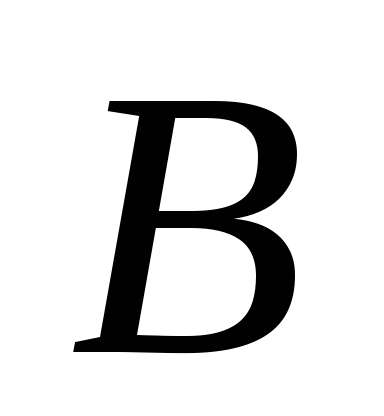 
nosník pôsobením dvoch sústredených síl a rovnomerne rozloženého zaťaženia. Vzhľadom na to:
|
|
Nájdite výslednicu rozloženého zaťaženia. Výsledný modul sa rovná
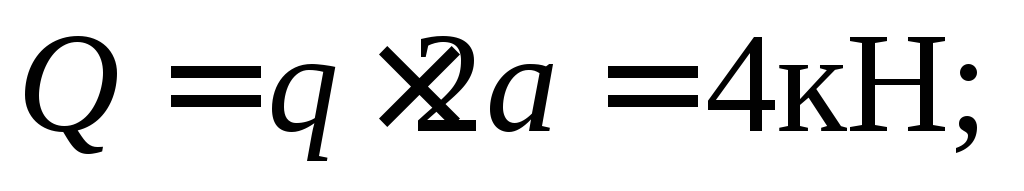
rameno sily 
vzhľadom na bod rovná sa 
Zvážte rovnováhu lúča. Napájací obvod je znázornený na obr. 1.33.
|
|
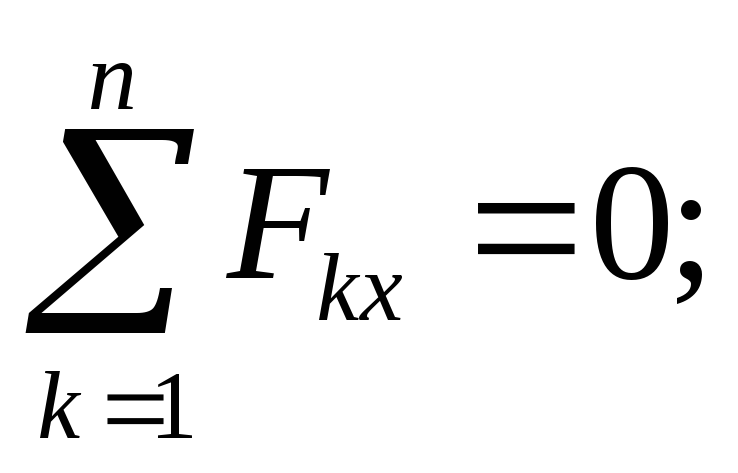
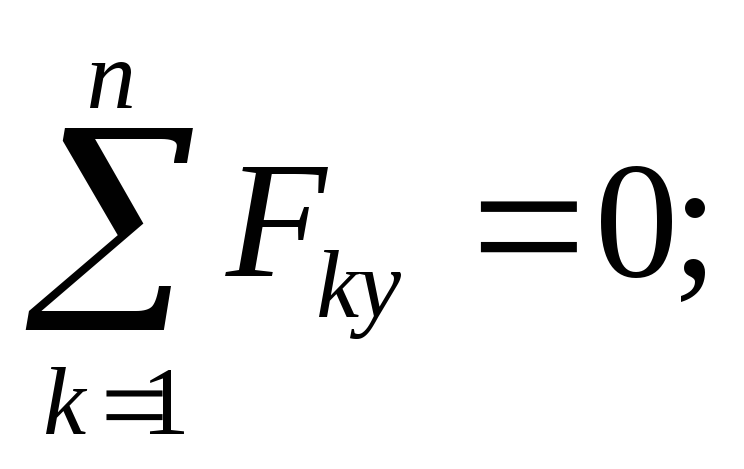
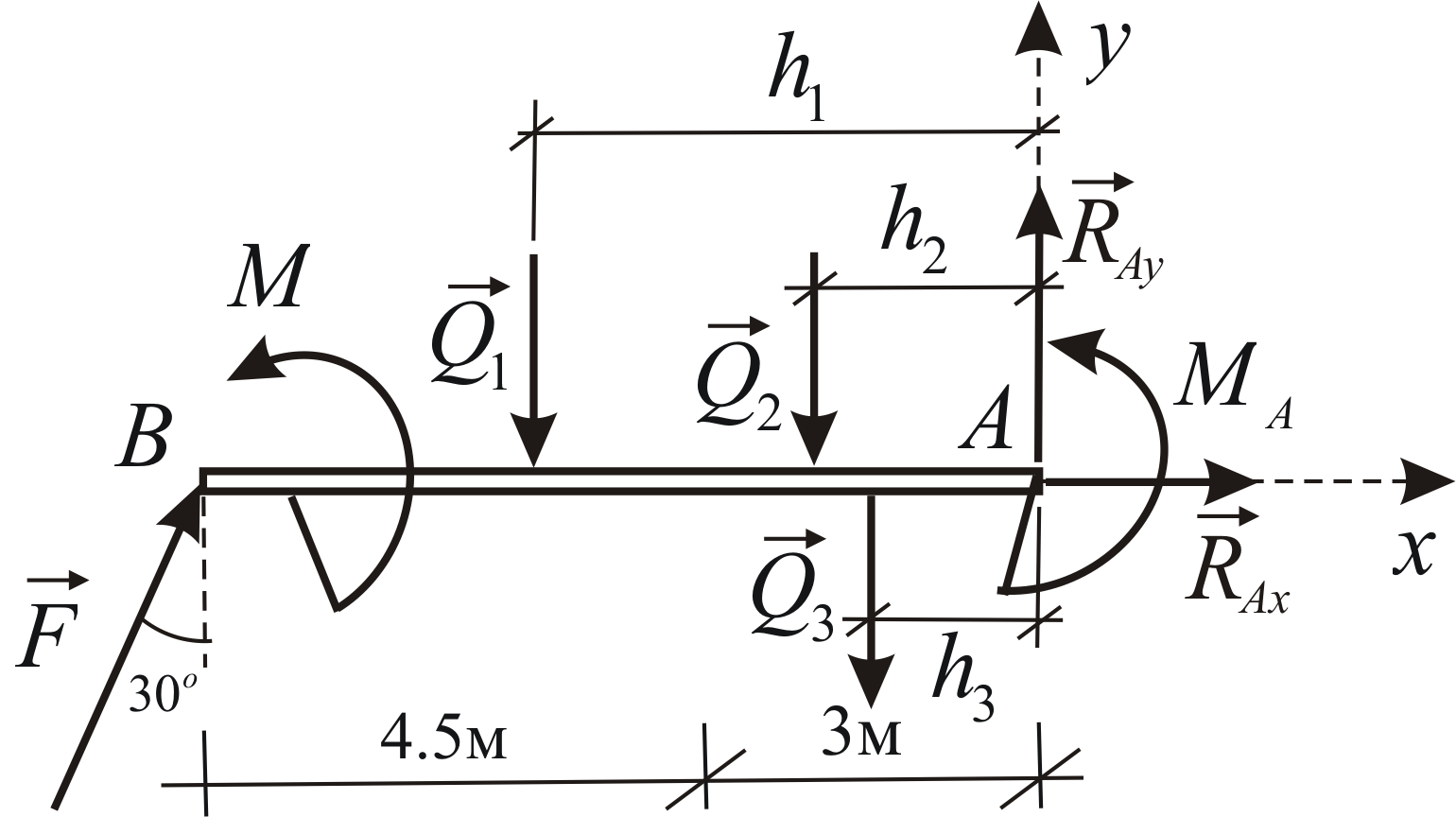
Príklad 1.6
Určte odozvu ukončenia konzolového nosníka pri pôsobení sústredenej sily, dvojice síl a rozloženého zaťaženia (obr. 1.34).
Nahraďte rozložené zaťaženie tromi sústredenými silami. Aby sme to dosiahli, rozdelíme diagram rozloženého zaťaženia na dva trojuholníky a obdĺžnik. nachádzame
Napájací obvod je znázornený na obr. 1.35.
|
|
|
|
Vypočítajte ramená výslednice vzhľadom na os 
Podmienky rovnováhy v posudzovanom prípade majú tvar:
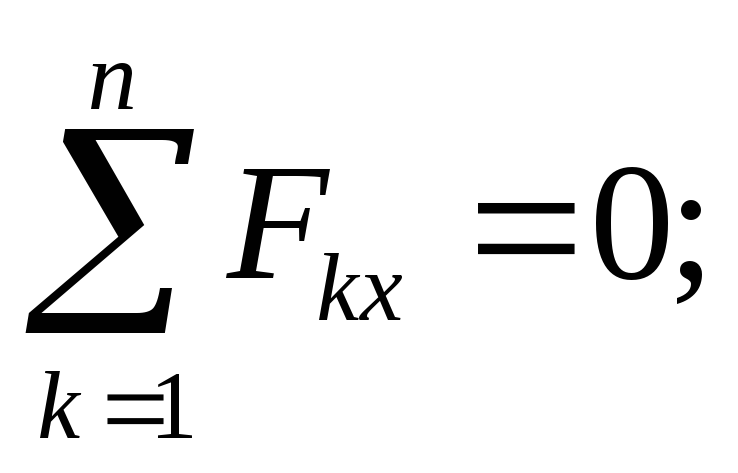
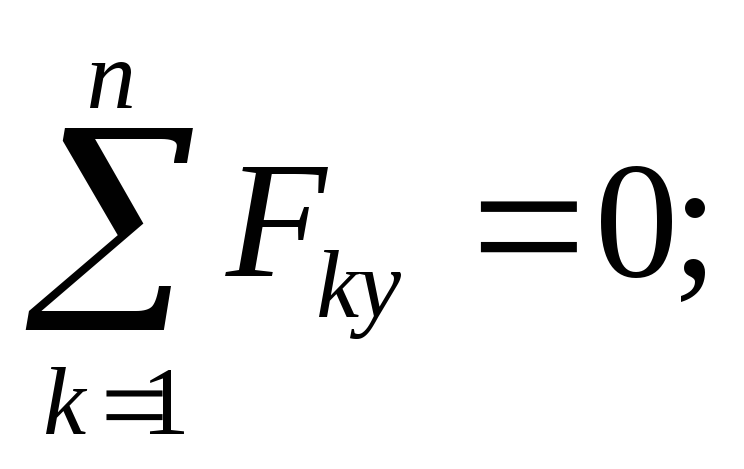
OTÁZKY NA SAMOKONTROLU:
1. Ako sa nazýva intenzita rozloženého zaťaženia?
2. Ako vypočítať modul výsledného rozloženého zaťaženia?
3. Ako vypočítať súradnicu bodu aplikácie výslednice rozloženej
naložiť?
4. Čo je modul a aká je súradnica bodu pôsobenia rovnomerne rozloženého zaťaženia?
5. Čo je modul a aká je súradnica bodu pôsobenia lineárne rozloženého zaťaženia?
Zo zbierky problémov I. V. Meshcherského: 4,28; 4,29; 4,30; 4,33; 4.34.
Z učebnice "TEORETICKÁ MECHANIKA - teória a prax": sady СР-2; SR-3.
PRAKTICKÉ ŠTÚDIE #4-5
Rozložené zaťaženie
Vplyv na časti, konštrukcie, prvky mechanizmov môže byť daný rozloženými zaťaženiami: v plochý systém intenzita pôsobenia je nastavená pozdĺž dĺžky konštrukcie, v priestorovom systéme - pozdĺž plochy.
Rozmer pre lineárne zaťaženie je N / m, pre zaťaženie rozložené na plochu - N / m 2, pre objem (napríklad pri zohľadnení vlastnej hmotnosti konštrukčných prvkov) - N / m 3.
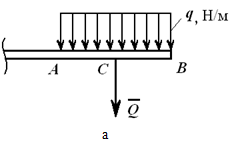
Napríklad na obrázku 1.23 je a zobrazené rovnomerne rozložené po dĺžke, merané v N / m. Toto zaťaženie môže byť nahradené koncentrovanou silou
Q = q∙AB[H],
aplikovaný v strede segmentu AB.
Obrázok 1.23, b zobrazuje rovnomerne klesajúce (rastúce) zaťaženie, ktoré môže byť nahradené výslednou silou
Q = qmax∙AB/2,
aplikovaný v bode C, a AC = 2/3AB.
V ľubovoľnom prípade znalosť funkcie q(x)(Obrázok 1.23, c), vypočítame ekvivalentnú silu
Táto sila pôsobí v ťažisku oblasti ohraničenej nad lúčom AB riadok q(x).
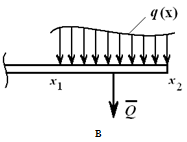
Obrázok 1.23
Príkladom je výpočet síl, ktoré rozbíjajú steny valca so stlačeným plynom. Určme výslednú tlakovú silu v sektore rúr pri intenzite q[N/m]; R je polomer potrubia, 2a– stredový uhol, os Vôl- os symetrie (obrázok 1.24).
Vyberme sektorový prvok s uhlom ∆φ a definovať silu ∆Q pôsobiace na prvok plochého oblúka:
∆Q = q ∙ ∆l = q ∙ R ∙ ∆φ. (1.14)
Obrázok 1.24
Vôl bude
∆Q x = q ∙ R ∙ ∆φ∙ cosφ. (1.15)
Vďaka symetrii rúrkového prvku (s oblúkom AB) okolo osi Vôl priemet výslednej sily na os Oj:
Qy = 0, t.j. Q = Qx, (1.16)
kde AB je tetiva, ktorá prekrýva konce oblúka.
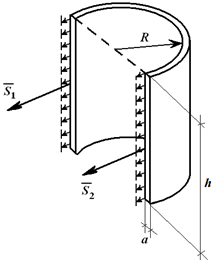
Pre valcovú nádobu s výškou h a vnútorný tlak P steny sú zaťažené intenzitou q = p [N/m, 2]. Ak je valec odrezaný v priemere (obrázok 1.25), potom sa rovná F = q ∙ d ∙ h (d– vnútorný priemer) alebo
F = p ∙ 2R ∙ h.
Trhanie balóna priemerom úsilia:
S 1 \u003d S 2 \u003d S;
2S = F;
S = p∙h∙R. (1.18)
Pri inžinierskych výpočtoch sa často stretávame so záťažami rozloženými pozdĺž daného povrchu podľa toho či onoho zákona. Zvážte niektoré z najjednoduchších príkladov rozložených síl ležiacich v rovnakej rovine.
Plochý systém rozložených síl je charakterizovaný svojou intenzitou q, t.j. hodnotou sily na jednotku dĺžky zaťažovaného segmentu. Intenzita sa meria v newtonoch vydelená metrom.
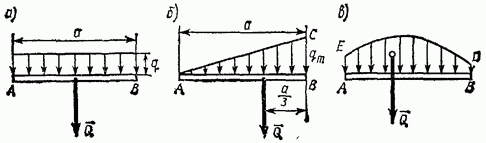
1) Sily rovnomerne rozložené pozdĺž priameho segmentu (obr. 69, a). Pre takýto systém síl má intenzita q konštantnú hodnotu. V statických výpočtoch možno tento systém síl nahradiť výslednicou
Modulo
V strede segmentu AB pôsobí sila Q.
2) Sily rozložené pozdĺž priamky podľa lineárneho zákona (obr. 69, b). Príkladom takéhoto zaťaženia môžu byť sily tlaku vody na hrádzu, ktoré majú najvyššia hodnota na dne a klesá na nulu na hladine vody. Pre tieto sily je intenzita q premenná hodnota rastúca od nuly do maximálnej hodnoty.Výsledka týchto síl Q sa určí podobne ako výslednica tiažových síl pôsobiacich na rovnomernú trojuholníkovú dosku ABC. Pretože hmotnosť homogénnej dosky je úmerná jej ploche, potom modulo,
Sila Q pôsobí vo vzdialenosti od strany BC trojuholníka ABC (pozri § 35, bod 2).
3) Sily rozložené pozdĺž priamky podľa ľubovoľného zákona (obr. 69, c). Výsledné Q takýchto síl, analogicky so silou gravitácie, sa v absolútnej hodnote rovná oblasti čísla ABDE, meranej vo vhodnej mierke, a prechádza cez ťažisko tejto oblasti ( otázka určenia ťažísk plôch bude posúdená v § 33).
4) Sily rovnomerne rozložené pozdĺž oblúka kruhu (obr. 70). Príkladom takýchto síl sú sily hydrostatického tlaku na bočné steny valcovej nádoby.
Nech je polomer oblúka , kde je os symetrie, pozdĺž ktorej os smerujeme.Sústava zbiehajúcich sa síl pôsobiacich na oblúk má výslednicu Q, smerujúcu v dôsledku symetrie pozdĺž osi, pričom
Na určenie hodnoty Q vyberieme prvok na oblúku, ktorého poloha je určená uhlom a dĺžkou Sila pôsobiaca na tento prvok sa číselne rovná a priemet tejto sily na os bude Potom
Ale z obr. 70 vidno, že Preto odvtedy
kde je dĺžka tetivy, ktorá pretína oblúk AB; q - intenzita.
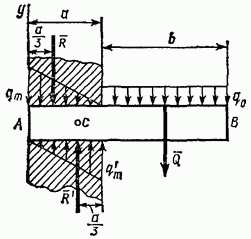
Úloha 27. Na konzolový nosník A B, ktorého rozmery sú naznačené na výkrese (obr. 71), pôsobí rovnomerne rozložené zaťaženie intenzity.
Riešenie. Vymieňame rozložené sily ich výslednice Q, R a R, kde podľa vzorcov (35) a (36)
a zostavte podmienky rovnováhy (33) pre paralelné sily pôsobiace na nosník
Nahradením ich hodnôt namiesto Q, R a R a riešením výsledných rovníc nakoniec nájdeme
Napríklad ak dostaneme a ak
Úloha 28. Valcový valec, ktorého výška je H a vnútorný priemer d, je naplnený plynom pod tlakom Hrúbka valcových stien valca je a. Určte ťahové napätia, ktorým tieto steny pôsobia v smeroch: 1) pozdĺžne a 2) priečne (napätie sa rovná pomeru ťahovej sily k ploche prierezu), pričom ho považujte za malé.
Riešenie. 1) Rozrežme valec rovinou kolmou na jeho os na dve časti a uvažujme o rovnováhe jednej z nich (obr.
72a). Pôsobí naň v smere osi valca tlaková sila na dno a sily rozložené po ploche prierezu (pôsobenie vyradenej polovice), ktorých výslednicu označíme Q. V rovnováhe
Vzdialenosť medzi sústredenými zaťaženiami je rovnaká, pričom vzdialenosť od začiatku rozpätia k prvému sústredenému zaťaženiu sa rovná vzdialenosti medzi sústredenými zaťaženiami. V tomto prípade sústredené zaťaženia tiež klesajú na začiatku a na konci rozpätia, ale v tomto prípade spôsobujú iba zvýšenie podporná reakcia extrémne sústredené zaťaženia neovplyvňujú hodnotu ohybových momentov a priehybu, a preto vo výpočtoch nosnosťštruktúry sa neberú do úvahy. Zvážte to na príklade podlahových nosníkov založených na preklade. Murivo, ktorý môže byť medzi prekladom a podlahovými nosníkmi a zároveň vytvára rovnomerne rozložené zaťaženie, nie je pre ľahké vnímanie znázornený.
Obrázok 1. Prevedenie sústredeného zaťaženia na ekvivalentné rovnomerne rozložené zaťaženie.
Ako je zrejmé z obrázku 1, určujúcim momentom je ohybový moment, ktorý sa používa pri pevnostných výpočtoch konštrukcií. Aby teda rovnomerne rozložené zaťaženie produkovalo rovnaký ohybový moment ako sústredené zaťaženie, musí sa vynásobiť príslušným koeficientom prechodu (koeficientom ekvivalencie). A tento koeficient je určený z podmienok rovnosti momentov. Myslím, že obrázok 1 to veľmi dobre ilustruje. A predsa je možné analýzou získaných závislostí odvodiť všeobecný vzorec na určenie koeficientu prechodu. Takže ak je počet aplikovaných koncentrovaných záťaží nepárny, t.j. jedno z koncentrovaných zaťažení nevyhnutne spadá do stredu rozpätia, potom na určenie koeficientu ekvivalencie môžete použiť vzorec:
γ = n/(n - 1) (305.1.1)
kde n je počet rozpätí medzi sústredenými zaťaženiami.
q ekv. = γ(n-1)Q/l (305.1.2)
kde (n-1) je počet koncentrovaných záťaží.
Niekedy je však vhodnejšie vykonať výpočty na základe počtu koncentrovaných zaťažení. Ak je táto veličina vyjadrená premennou m, potom
y = (m+1)/m (305.1.3)
V tomto prípade sa ekvivalentné rovnomerne rozložené zaťaženie bude rovnať:
q ekv. = γmQ/l (305.1.4)
Keď je počet sústredených záťaží párny, t.j. žiadne zo sústredených zaťažení nespadá do stredu rozpätia, potom hodnotu koeficientu možno brať ako ďalšiu nepárnu hodnotu počtu sústredených zaťažení. Vo všeobecnosti, v závislosti od špecifikovaných podmienok zaťaženia, môžu byť použité tieto prevodné koeficienty:
γ = 2- ak na uvažovanú konštrukciu dopadá len jedno sústredené zaťaženie v strede prekladu, napríklad trám.
y = 1,33- pre nosník, na ktorý pôsobia 2 alebo 3 sústredené zaťaženia;
y = 1,2- pre nosník, na ktorý pôsobí 4 alebo 5 sústredených zaťažení;
y = 1,142- pre nosník, na ktorý pôsobí 6 alebo 7 sústredených zaťažení;
y = 1,11- pre nosník, na ktorý pôsobí 8 alebo 9 sústredených zaťažení.
Možnosť 2
Vzdialenosť medzi sústredenými zaťaženiami je rovnaká, pričom vzdialenosť od začiatku rozpätia k prvému sústredenému zaťaženiu sa rovná polovici vzdialenosti medzi sústredenými zaťaženiami. V tomto prípade koncentrované zaťaženie nespadá na začiatok a koniec rozpätia.
Obrázok 2. Hodnoty koeficientov prechodu pre 2. variant aplikácie sústredeného zaťaženia.
Ako je zrejmé z obrázku 2, pri tejto možnosti zaťaženia bude hodnota koeficientu prechodu oveľa menšia. Takže napríklad pri párnom počte sústredených zaťažení možno koeficient prechodu vo všeobecnosti považovať za rovný jednotke. Pri nepárnom počte sústredených zaťažení možno na určenie koeficientu ekvivalencie použiť vzorec:
γ = (m+7)/(m+6) (305.2.1)
kde m je počet sústredených zaťažení.
V tomto prípade sa ekvivalentné rovnomerne rozložené zaťaženie bude stále rovnať:
q ekv. = γmQ/l (305.1.4)
Vo všeobecnosti, v závislosti od špecifikovaných podmienok zaťaženia, môžu byť použité tieto prevodné koeficienty:
γ = 2- ak na posudzovanú konštrukciu dopadá napríklad len jedno sústredené zaťaženie v strede prekladu a či podlahové trámy dopadajú na začiatok alebo koniec rozpätia alebo sú umiestnené ľubovoľne ďaleko od začiatku a konca rozpätia, v tomto prípade je to jedno. A to je dôležité pri určovaní koncentrovaného zaťaženia.
γ = 1- ak na uvažovanú konštrukciu pôsobí párny počet zaťažení.
y = 1,11- pre nosník, na ktorý pôsobia 3 sústredené zaťaženia;
y = 1,091- pre nosník, na ktorý pôsobí 5 sústredených zaťažení;
y = 1,076- pre nosník, na ktorý pôsobí 7 sústredených zaťažení;
y = 1,067- pre nosník, na ktorý pôsobí 9 sústredených zaťažení.
Napriek zložitej definícii sú koeficienty ekvivalencie veľmi jednoduché a pohodlné. Keďže rozložené zaťaženie pôsobiace na štvorcový alebo lineárny meter je vo výpočtoch veľmi často známe, aby sa rozložené zaťaženie nepremenilo najskôr na sústredené a potom opäť na ekvivalentne rozložené, stačí jednoducho vynásobiť hodnotu rozložené zaťaženie príslušným koeficientom. Napríklad na podlahu bude pôsobiť normatívne rozložené zaťaženie 400 kg / m 2, zatiaľ čo vlastná hmotnosť podlahy bude ďalších 300 kg / m 2. Potom by pri dĺžke podlahového nosníka 6 m mohlo na preklad pôsobiť rovnomerne rozložené zaťaženie q = 6(400 + 300)/2 = 2100 kg/m. A potom, ak je v strede rozpätia iba jeden podlahový nosník, potom γ = 2 a
q ekv. = γq = 2q (305.2.2)
Ak nie je splnená žiadna z vyššie uvedených dvoch podmienok, potom nie je možné použiť koeficienty prechodu v ich čistej forme, musíte pridať niekoľko ďalších koeficientov, ktoré zohľadňujú vzdialenosť k trámom, ktoré na začiatku nespadajú a koniec rozpätia prekladu, ako aj možnú asymetriu aplikácie sústredených zaťažení. V zásade je možné takéto koeficienty odvodiť, v každom prípade však budú vo všetkých prípadoch redukujúce, ak uvažujeme 1. možnosť zaťaženia a v 50 % prípadov, ak uvažujeme 2. možnosť zaťaženia, t.j. hodnoty takýchto koeficientov budú< 1. А потому для упрощения расчетов, а заодно и для большего запаса по прочности рассчитываемой конструкции вполне хватит коэффициентов, приведенных при первых двух вариантах загружения.
Rozložené zaťaženie
Vplyv na časti, konštrukcie, prvky mechanizmov je možné nastaviť rozloženými zaťaženiami: v plochom systéme je intenzita pôsobenia nastavená pozdĺž dĺžky konštrukcie, v priestorovom systéme - po ploche.
Rozmer pre lineárne zaťaženie je N / m, pre zaťaženie rozložené na plochu - N / m 2, pre objem (napríklad pri zohľadnení vlastnej hmotnosti konštrukčných prvkov) - N / m 3.
Napríklad na obrázku 1.23 je a zobrazené rovnomerne rozložené po dĺžke, merané v N / m. Toto zaťaženie môže byť nahradené koncentrovanou silou
Q = q∙AB[H],
aplikovaný v strede segmentu AB.
Obrázok 1.23, b zobrazuje rovnomerne klesajúce (rastúce) zaťaženie, ktoré môže byť nahradené výslednou silou
Q = qmax∙AB/2,
aplikovaný v bode C, a AC = 2/3AB.
V ľubovoľnom prípade znalosť funkcie q(x)(Obrázok 1.23, c), vypočítame ekvivalentnú silu
Táto sila pôsobí v ťažisku oblasti ohraničenej nad lúčom AB riadok q(x).
Obrázok 1.23
Príkladom je výpočet síl, ktoré rozbíjajú steny valca so stlačeným plynom. Určme výslednú tlakovú silu v sektore rúr pri intenzite q[N/m]; R je polomer potrubia, 2a– stredový uhol, os Vôl- os symetrie (obrázok 1.24).
Vyberme sektorový prvok s uhlom ∆φ a definovať silu ∆Q pôsobiace na prvok plochého oblúka:
∆Q = q ∙ ∆l = q ∙ R ∙ ∆φ. (1.14)
Obrázok 1.24
Vôl bude
∆Q x = q ∙ R ∙ ∆φ∙ cosφ. (1.15)
Vďaka symetrii rúrkového prvku (s oblúkom AB) okolo osi Vôl priemet výslednej sily na os Oj:
Qy = 0, t.j. Q = Qx, (1.16)
kde AB je tetiva, ktorá prekrýva konce oblúka.
Pre valcovú nádobu s výškou h a vnútorný tlak P steny sú zaťažené intenzitou q = p [N/m, 2]. Ak je valec odrezaný v priemere (obrázok 1.25), potom sa rovná F = q ∙ d ∙ h (d– vnútorný priemer) alebo
F = p ∙ 2R ∙ h.
Trhanie balóna priemerom úsilia:
S 1 \u003d S 2 \u003d S;
2S = F;
S = p∙h∙R. (1.18)
