Σπίτι Αριθμομηχανές

Ανομοιόμορφα κατανεμημένο φορτίο. Κατανεμημένο φορτίο

Οι επιφανειακές και ογκομετρικές δυνάμεις αντιπροσωπεύουν ένα φορτίο που κατανέμεται σε μια συγκεκριμένη επιφάνεια ή όγκο. Ένα τέτοιο φορτίο δίνεται από την ένταση, που είναι η δύναμη ανά μονάδα κάποιου όγκου, ή κάποιας περιοχής ή κάποιου μήκους.

Ιδιαίτερη θέση στην επίλυση ορισμένων πρακτικά ενδιαφέροντων προβλημάτων κατέχει η περίπτωση ενός επίπεδου κατανεμημένου φορτίου που εφαρμόζεται κατά μήκος της κανονικής σε μια συγκεκριμένη δοκό. Εάν ο άξονας κατευθύνεται κατά μήκος της δοκού 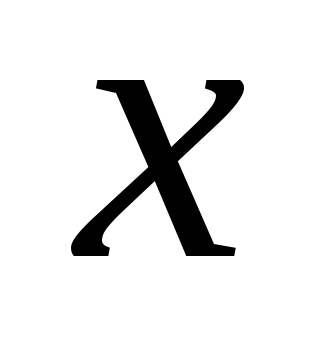, τότε η ένταση θα είναι συνάρτηση της συντεταγμένης 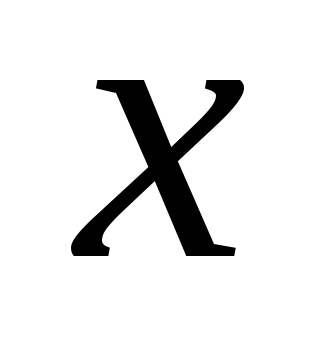και μετριέται σε N/m. Η ένταση αντιπροσωπεύει τη δύναμη ανά μονάδα μήκους.

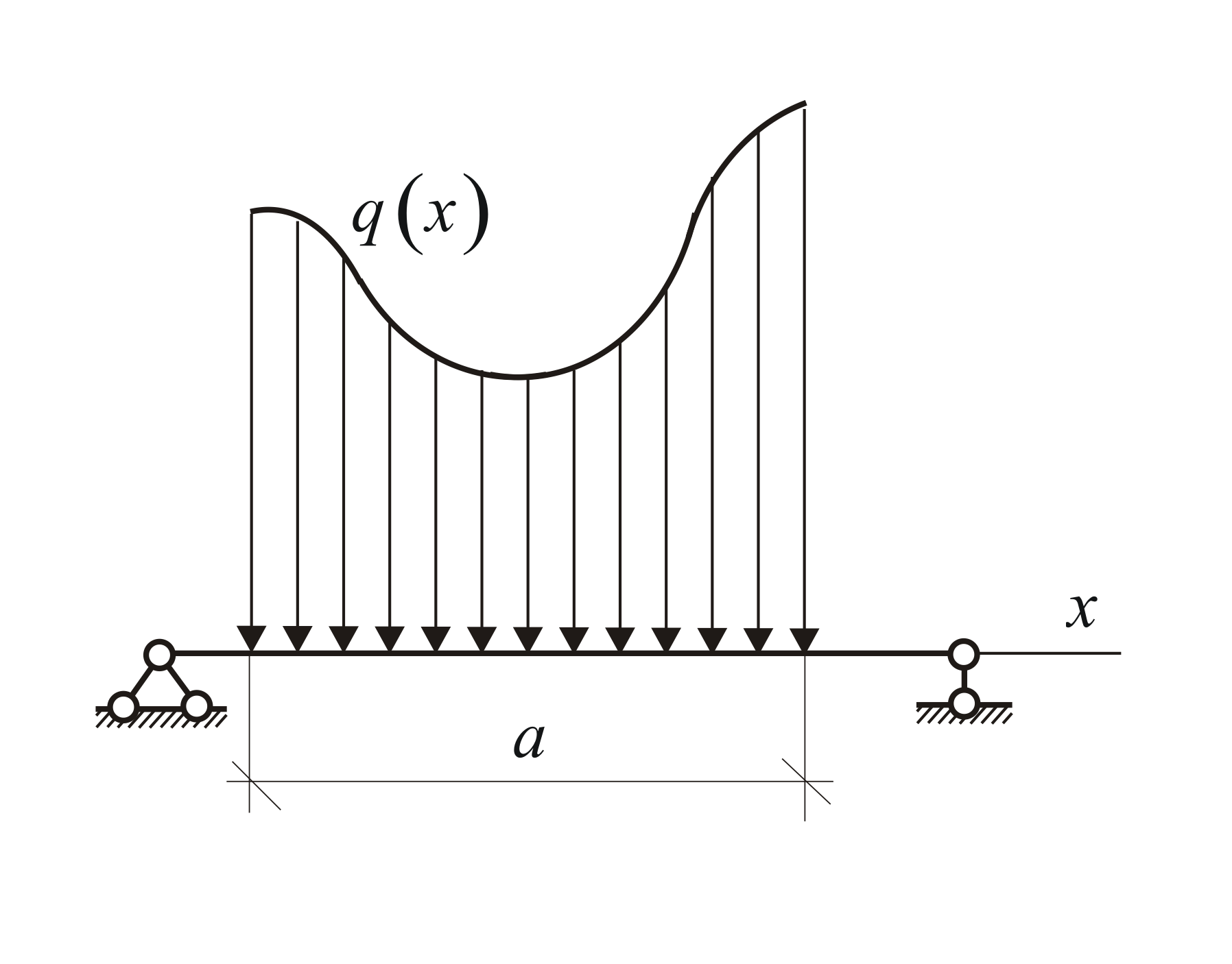
Ένα επίπεδο σχήμα που οριοθετείται από μια δοκό και ένα γράφημα έντασης φορτίου ονομάζεται διάγραμμα κατανεμημένου φορτίου (Εικ. 1.28). Εάν, λόγω της φύσης του προβλήματος που επιλύεται, οι παραμορφώσεις μπορούν να αγνοηθούν, π.χ. Εάν το σώμα μπορεί να θεωρηθεί απολύτως συμπαγές, τότε το κατανεμημένο φορτίο μπορεί (και πρέπει) να αντικατασταθεί από ένα προκύπτον φορτίο.

Ας χωρίσουμε τη δέσμη σε μήκη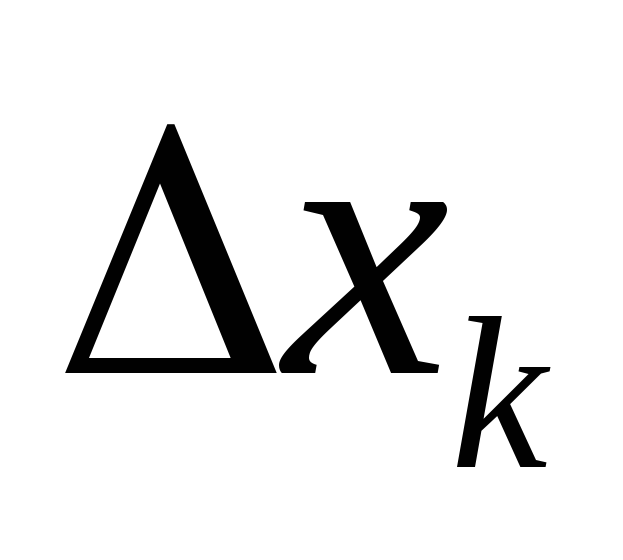

, σε καθένα από τα οποία θα υποθέσουμε ότι η ένταση είναι σταθερή και ίση

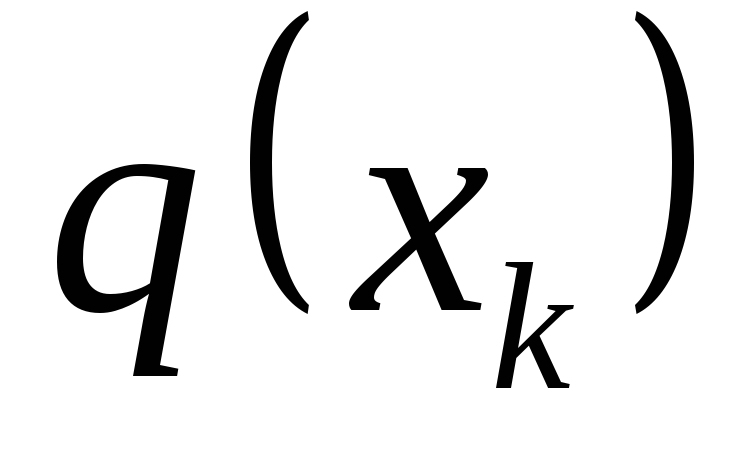, Οπου 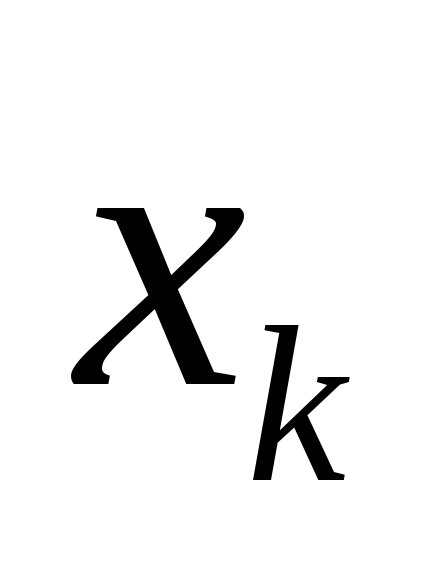– συντεταγμένες του τμήματος

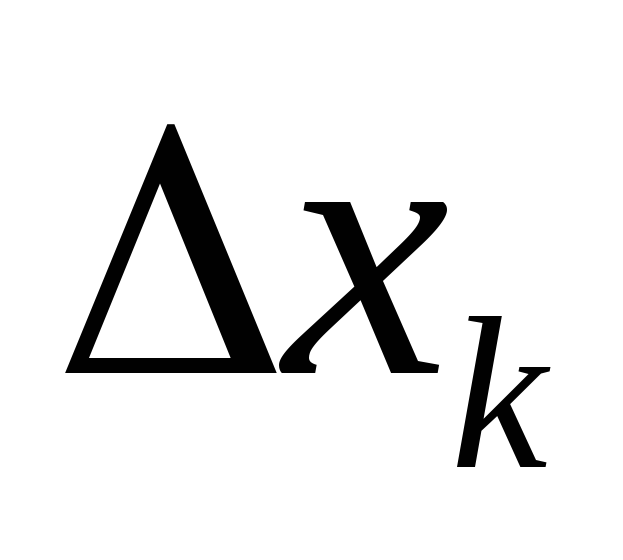. Σε αυτή την περίπτωση, η καμπύλη έντασης αντικαθίσταται από μια διακεκομμένη γραμμή και το φορτίο ανά τμήμα

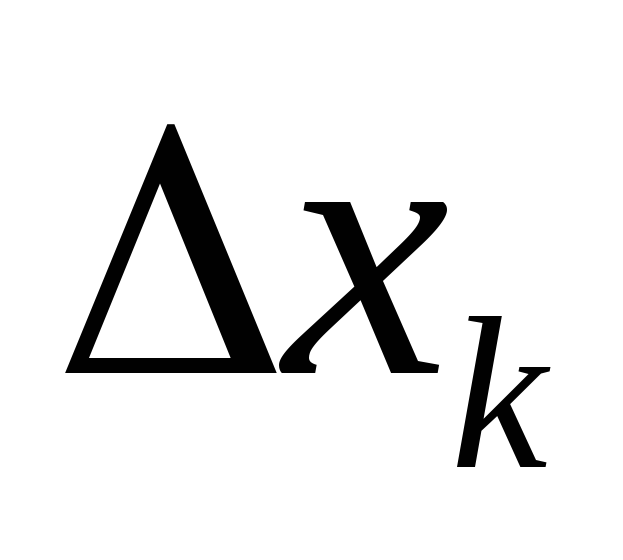, αντικαθίσταται από συγκεντρωμένη δύναμη

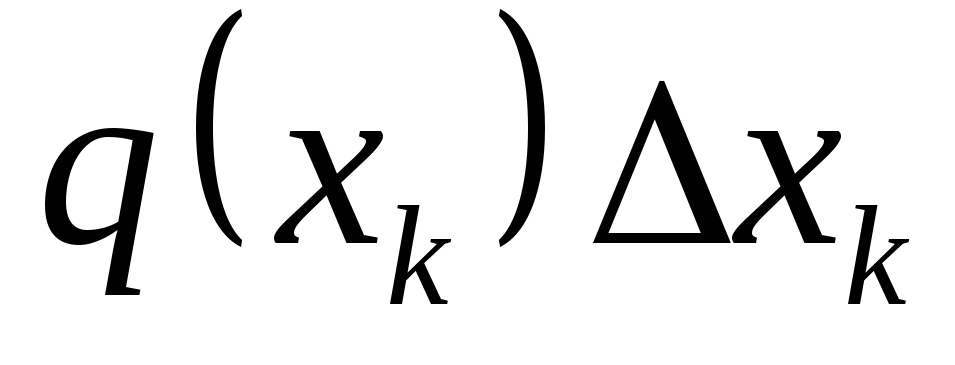, που εφαρμόζεται στο σημείο 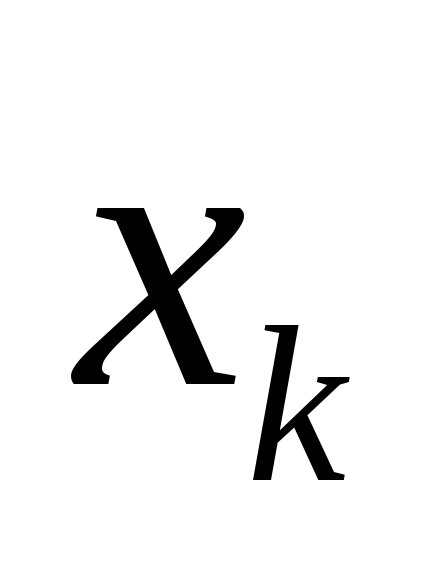(Εικ. 1.29). Το προκύπτον σύστημα παράλληλων δυνάμεων έχει αποτέλεσμα ίσο με το άθροισμα των δυνάμεων που ασκούνται σε καθένα από τα τμήματα, που εφαρμόζεται στο κέντρο των παράλληλων δυνάμεων.

Είναι σαφές ότι μια τέτοια αναπαράσταση περιγράφει την πραγματική κατάσταση με μεγαλύτερη ακρίβεια, όσο μικρότερο είναι το τμήμα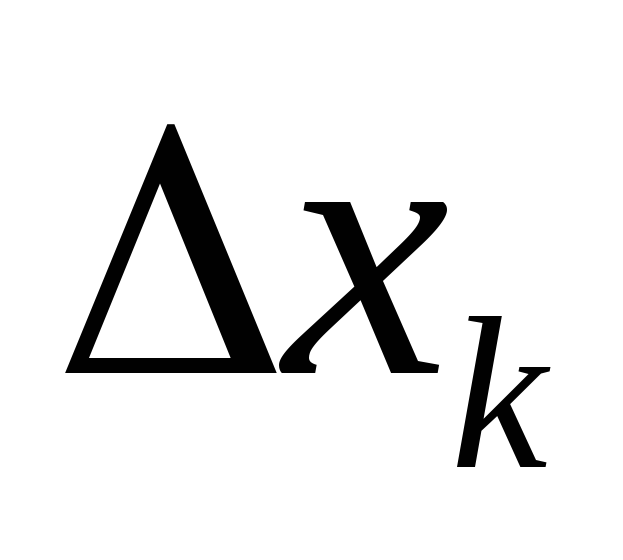

, δηλ. τόσο μεγαλύτερος είναι ο αριθμός των τμημάτων . Λαμβάνουμε το ακριβές αποτέλεσμα περνώντας στο όριο στο μήκος του τμήματος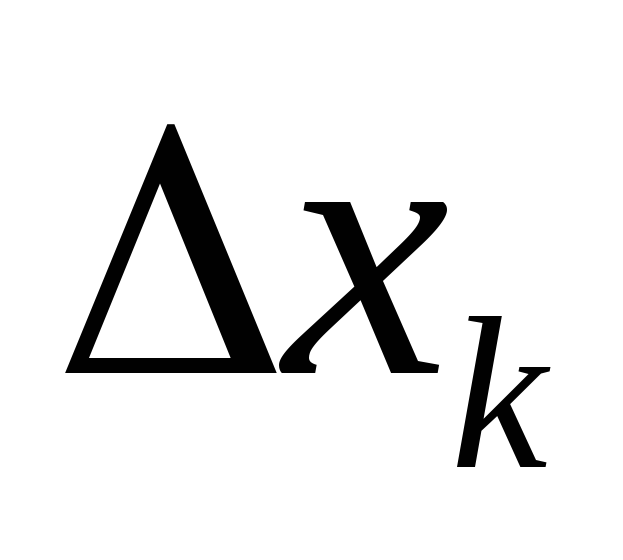

τείνει στο μηδέν. Το όριο που προκύπτει ως αποτέλεσμα της περιγραφόμενης διαδικασίας είναι αναπόσπαστο. Έτσι, για το συντελεστή του προκύπτοντος λαμβάνουμε:

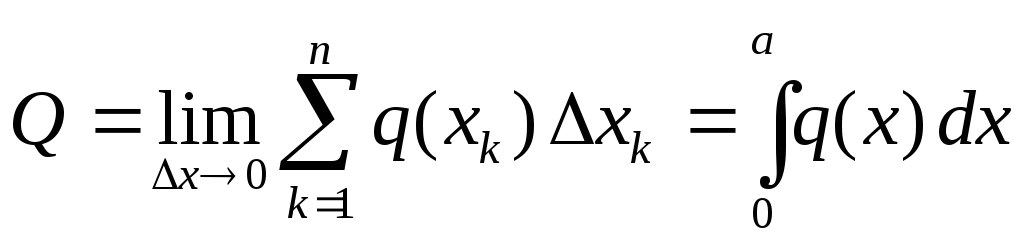
Να προσδιορίσετε τις συντεταγμένες ενός σημείου Εφαρμογή του αποτελέσματος χρησιμοποιούμε το θεώρημα του Varignon:

εάν ένα σύστημα δυνάμεων έχει αποτέλεσμα, τότε η ροπή του προκύπτοντος σε σχέση με οποιοδήποτε κέντρο (οποιονδήποτε άξονα) είναι ίση με το άθροισμα των ροπών όλων των δυνάμεων του συστήματος σε σχέση με αυτό το κέντρο (αυτός ο άξονας)

Γράψιμο αυτού του θεωρήματος για ένα σύστημα δυνάμεων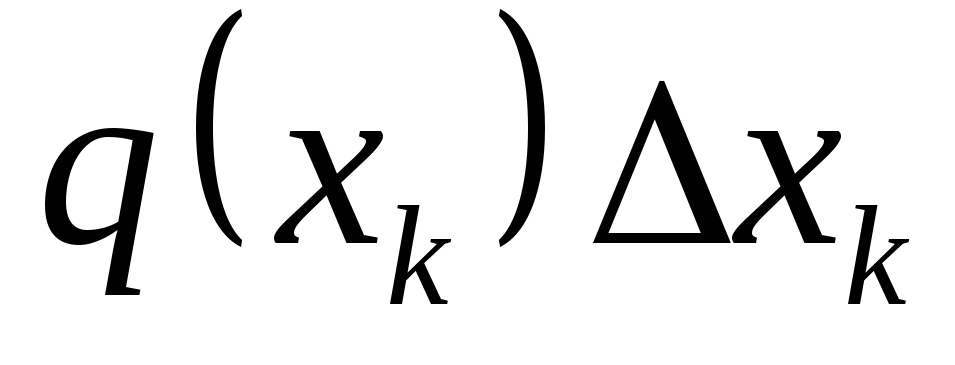

σε προβολές στον άξονα 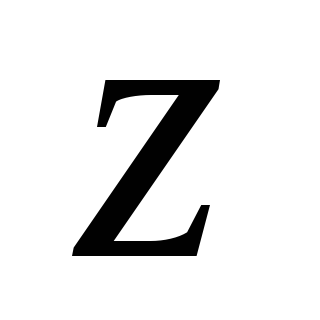και περνώντας στο όριο όταν το μήκος των τμημάτων τείνει στο μηδέν, παίρνουμε:

Προφανώς, η μονάδα του προκύπτοντος είναι αριθμητικά ίση με την περιοχή του διαγράμματος κατανεμημένου φορτίου και το σημείο εφαρμογής της συμπίπτει με το κέντρο βάρους μιας ομοιογενούς πλάκας που έχει το σχήμα ενός διαγράμματος κατανεμημένου φορτίου.

Ας σημειώσουμε δύο περιπτώσεις που εμφανίζονται συχνά.

,

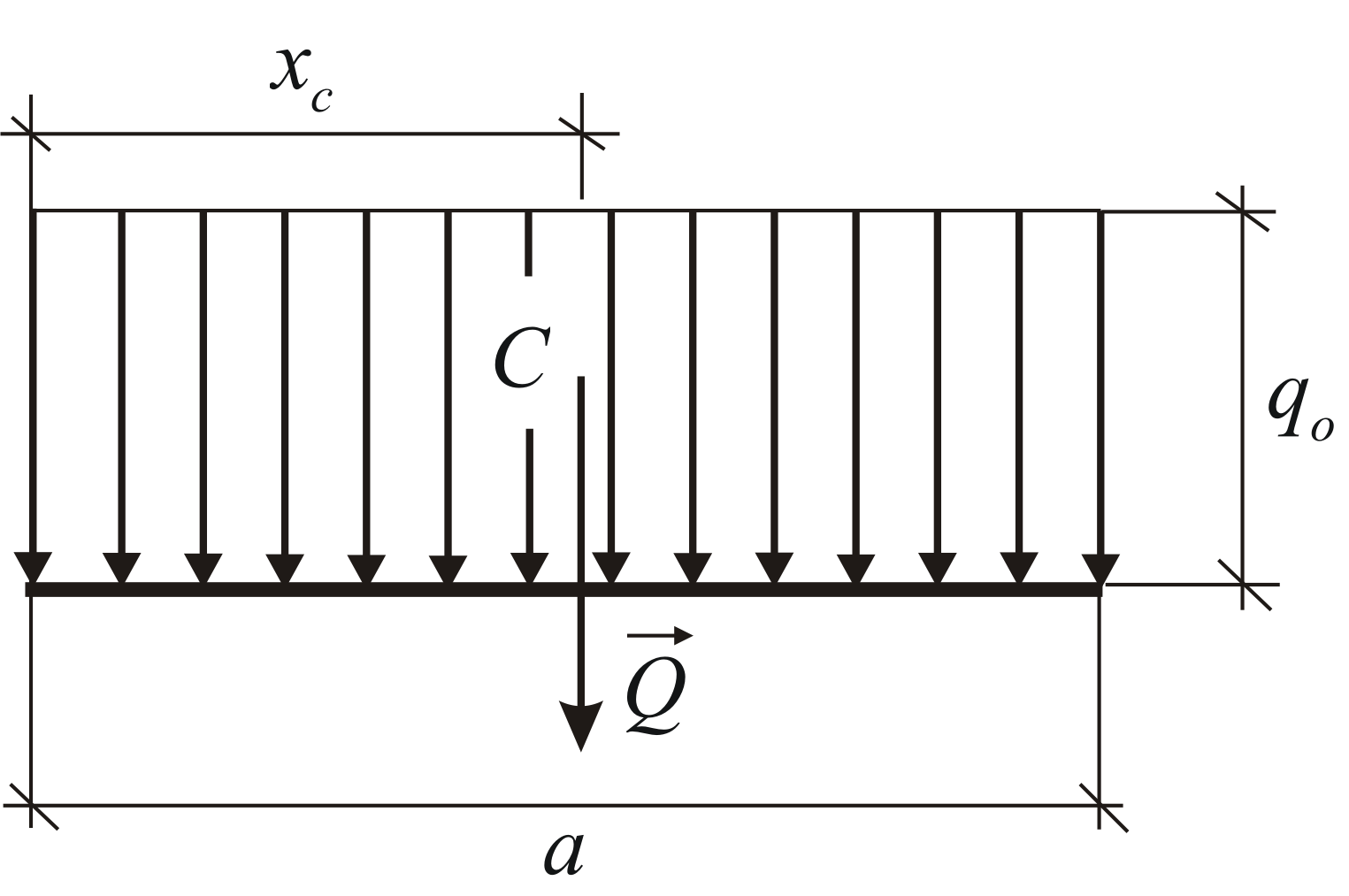
(Εικ. 1.30). Η ενότητα του προκύπτοντος και η συντεταγμένη του σημείου εφαρμογής της καθορίζονται από τους τύπους:

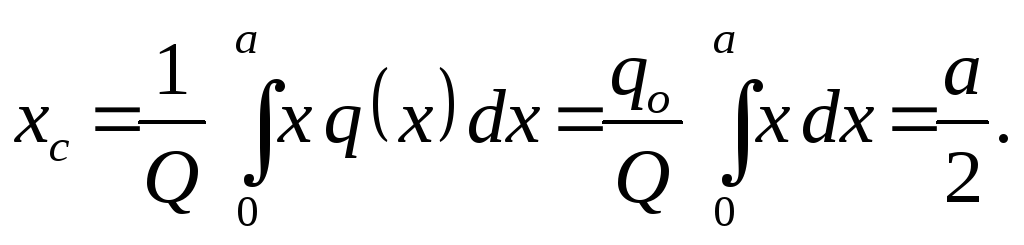
Στην πρακτική της μηχανικής, ένα τέτοιο φορτίο συμβαίνει αρκετά συχνά. Στις περισσότερες περιπτώσεις, το βάρος και το φορτίο ανέμου μπορούν να θεωρηθούν ομοιόμορφα κατανεμημένα.

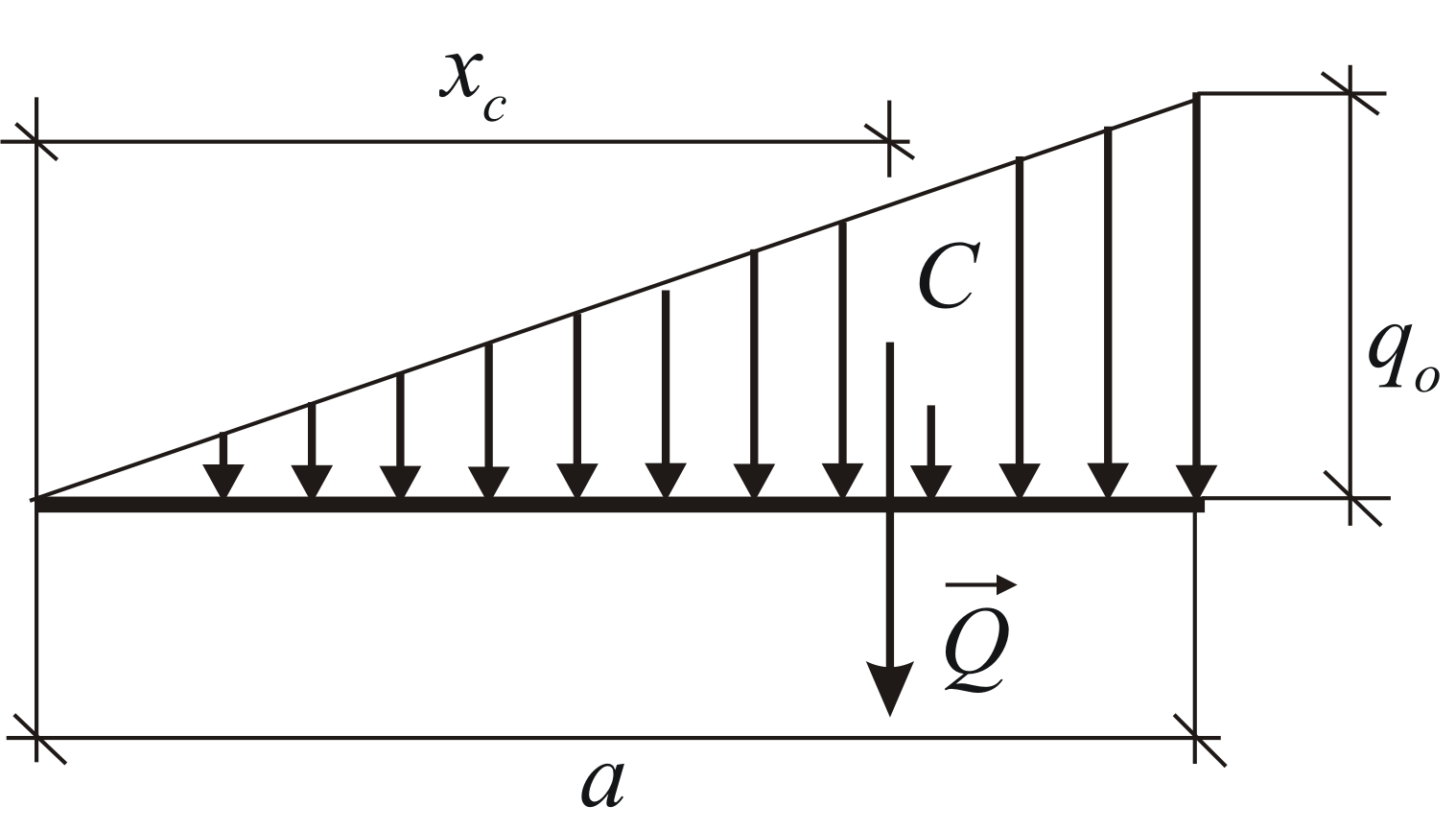
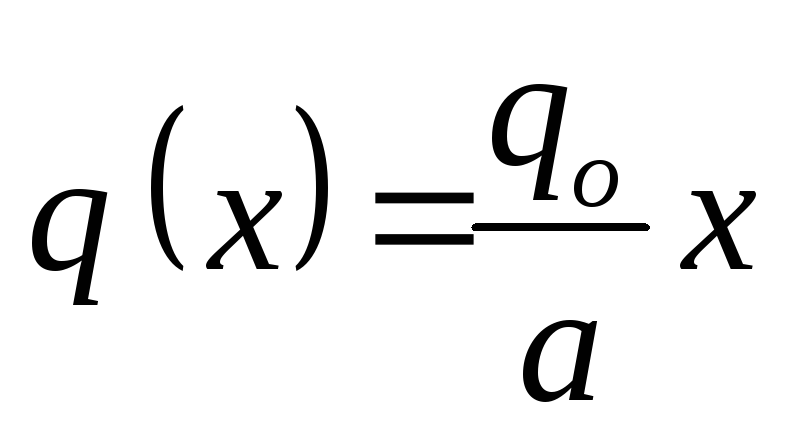(Εικ. 1.31). Σε αυτήν την περίπτωση:

Συγκεκριμένα, η πίεση του νερού σε έναν κατακόρυφο τοίχο είναι ευθέως ανάλογη με το βάθος .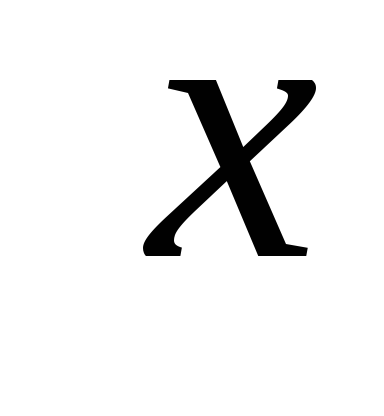

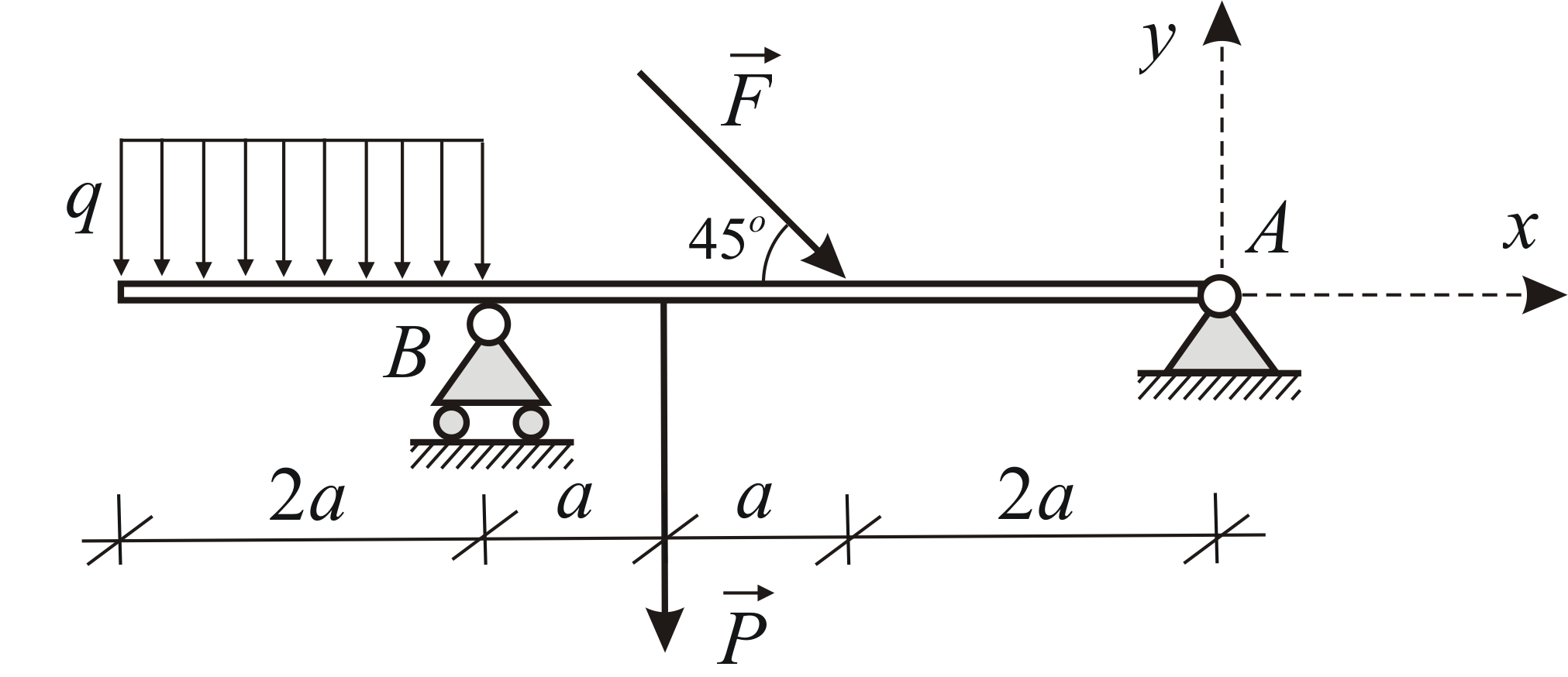
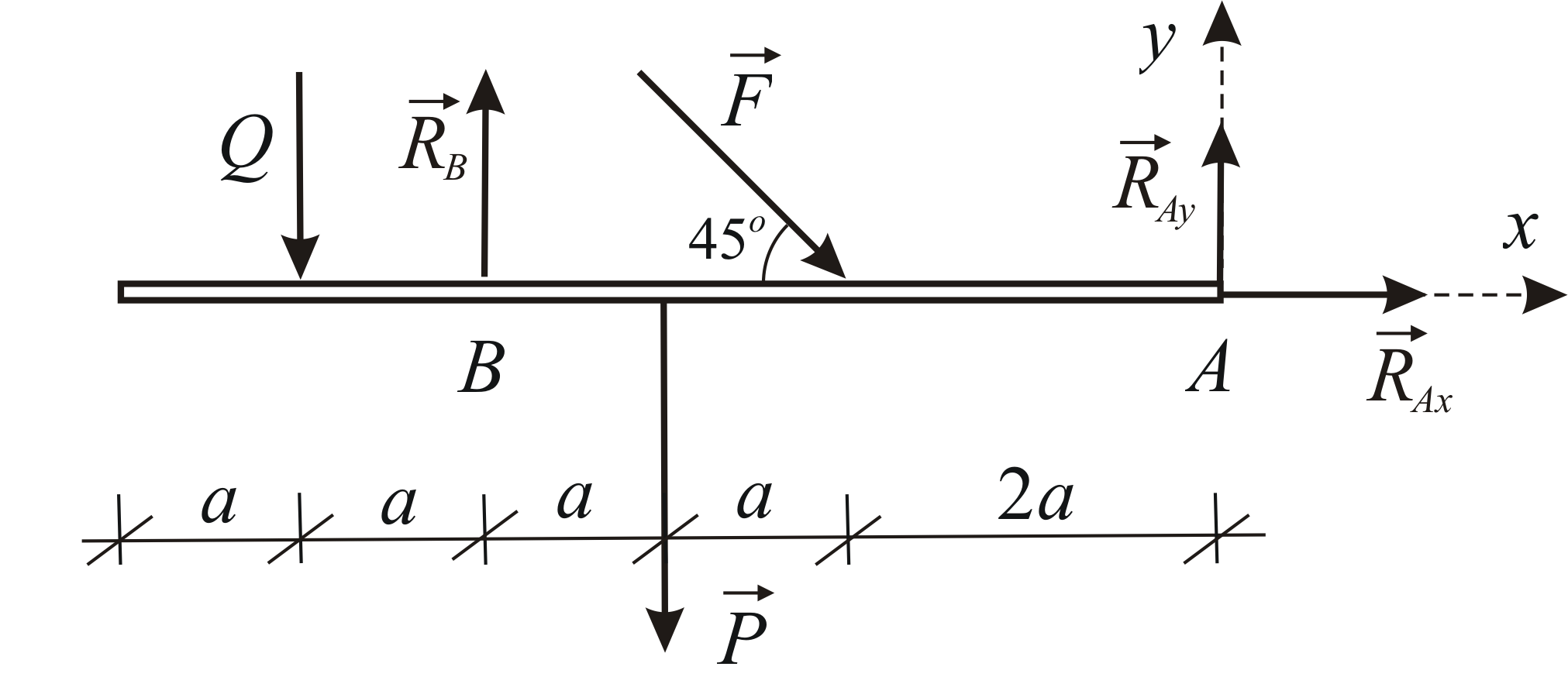
Παράδειγμα 1.5

Προσδιορίστε τις αντιδράσεις υποστήριξης Και 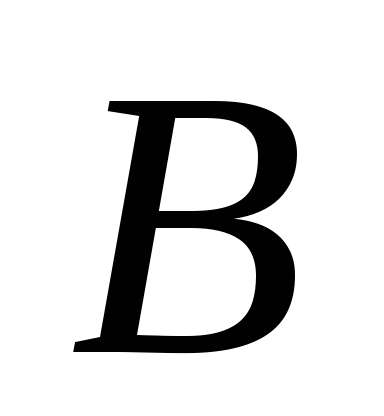δοκός υπό τη δράση δύο συγκεντρωμένων δυνάμεων και ενός ομοιόμορφα κατανεμημένου φορτίου. Δεδομένος:

Ας βρούμε το αποτέλεσμα του κατανεμημένου φορτίου. Ο συντελεστής του προκύπτοντος είναι ίσος με

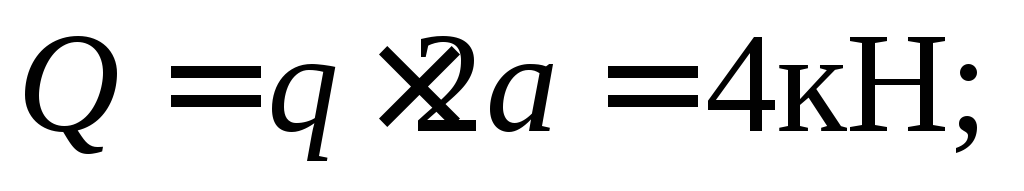
δύναμη ώμου σε σχέση με το σημείο ισοδυναμεί

Θεωρήστε την ισορροπία μιας δέσμης. Το κύκλωμα ισχύος φαίνεται στο Σχ. 1.33.

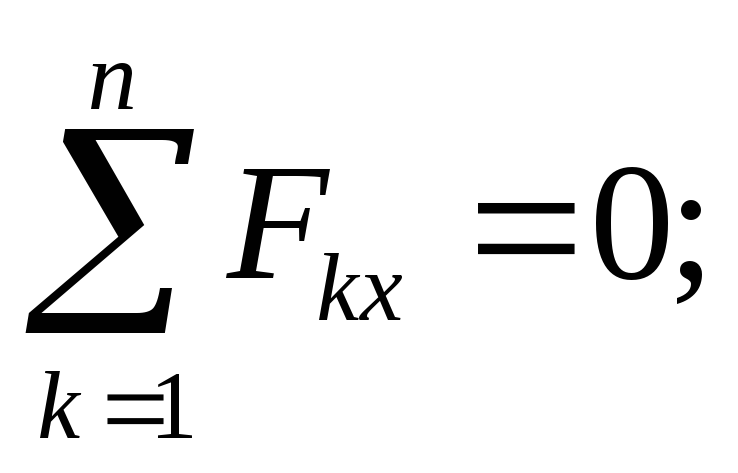
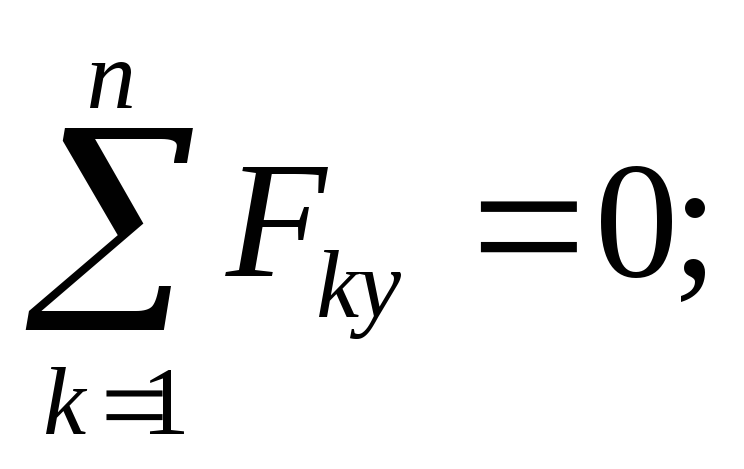
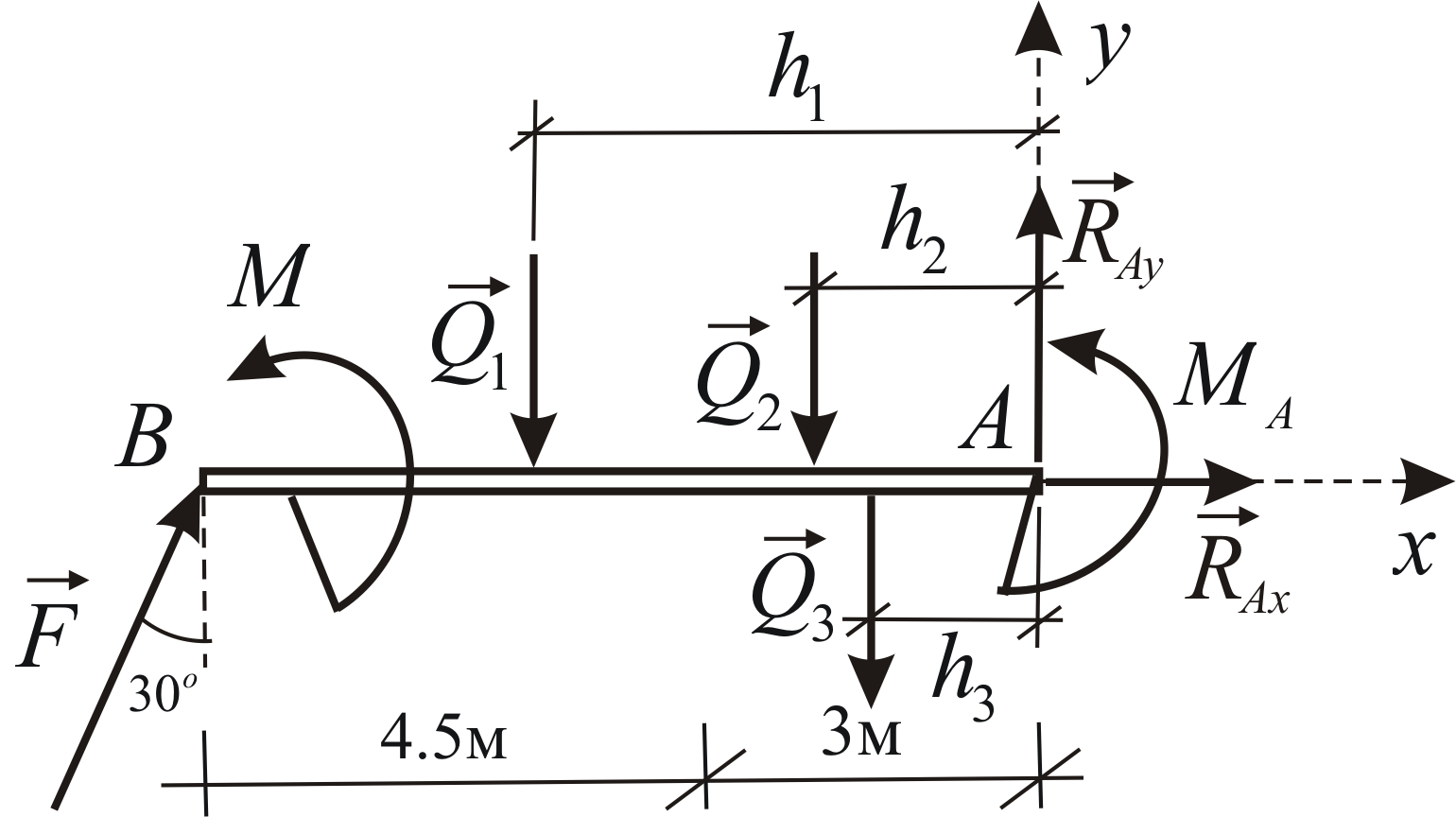
Παράδειγμα 1.6

Προσδιορίστε την αντίδραση της ενσωμάτωσης μιας δοκού προβόλου υπό τη δράση μιας συγκεντρωμένης δύναμης, ενός ζεύγους δυνάμεων και ενός κατανεμημένου φορτίου (Εικ. 1.34).

Ας αντικαταστήσουμε το κατανεμημένο φορτίο με τρεις συγκεντρωμένες δυνάμεις. Για να το κάνετε αυτό, διαιρέστε το διάγραμμα του κατανεμημένου φορτίου σε δύο τρίγωνα και ένα ορθογώνιο. Βρίσκουμε

Το κύκλωμα ισχύος φαίνεται στο Σχ. 1,35.

Ας υπολογίσουμε τους βραχίονες των προκυπτόντων σε σχέση με τον άξονα

Οι συνθήκες ισορροπίας στην υπό εξέταση περίπτωση έχουν τη μορφή:

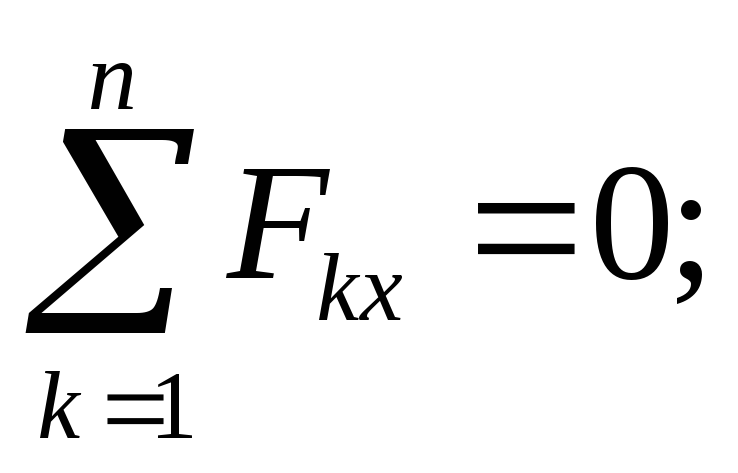
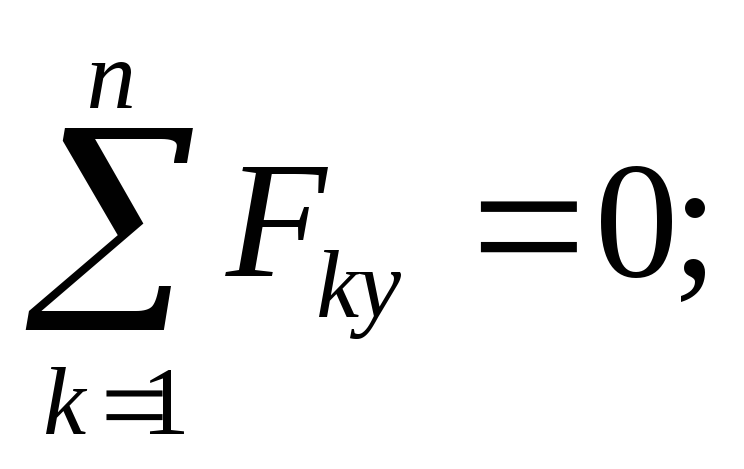
ΕΡΩΤΗΣΕΙΣ ΓΙΑ ΑΥΤΟΕΛΕΓΧΟ:

1. Ποια είναι η κατανεμημένη ένταση φορτίου;

2. Πώς να υπολογίσετε το μέτρο του προκύπτοντος κατανεμημένου φορτίου;

3. Πώς υπολογίζεται η συντεταγμένη του σημείου εφαρμογής του προκύπτοντος κατανεμημένου

φορτώνω?

4. Ποιο είναι το μέτρο και ποια η συντεταγμένη του σημείου εφαρμογής ενός ομοιόμορφα κατανεμημένου φορτίου;

5. Τι είναι το μέτρο και ποια η συντεταγμένη του σημείου εφαρμογής ενός γραμμικά κατανεμημένου φορτίου;

Από τη συλλογή προβλημάτων του I.V. Meshchersky: 4.28; 4.29; 4.30; 4.33; 4.34.

Από το σχολικό βιβλίο «ΘΕΩΡΗΤΙΚΗ ΜΗΧΑΝΙΚΗ - θεωρία και πράξη»: κιτ SR-2; SR-3.

ΠΡΑΚΤΙΚΑ ΜΑΘΗΜΑΤΑ Νο. 4-5

Κατανεμημένα φορτία

Η πρόσκρουση σε μέρη, δομές και στοιχεία μηχανισμών μπορεί να προσδιοριστεί με κατανεμημένα φορτία: in επίπεδο σύστημαη ένταση της δράσης τίθεται σε όλο το μήκος της δομής, σε ένα χωρικό σύστημα - κατά μήκος της περιοχής.

Η διάσταση για ένα γραμμικό φορτίο είναι N/m, για ένα φορτίο που κατανέμεται σε μια περιοχή - N/m 2, για ένα ογκομετρικό φορτίο (για παράδειγμα, όταν λαμβάνεται υπόψη το νεκρό βάρος των δομικών στοιχείων) - N/m 3.

Για παράδειγμα, στο Σχήμα 1.23, το a φαίνεται ομοιόμορφα κατανεμημένο κατά μήκος, μετρημένο σε N/m. Αυτό το φορτίο μπορεί να αντικατασταθεί από μια συγκεντρωμένη δύναμη

Q = q ∙ AB[Η],

εφαρμόζεται στη μέση του τμήματος ΑΒ.

Το σχήμα 1.23, b δείχνει ένα ομοιόμορφα μειούμενο (αυξανόμενο) φορτίο, το οποίο μπορεί να αντικατασταθεί από μια προκύπτουσα δύναμη

Q = q max ∙AB/2,

εφαρμόζεται στο σημείο ντο, και AC = 2/3AB.

Σε μια αυθαίρετη περίπτωση, γνωρίζοντας τη λειτουργία q(x)(Εικόνα 1.23, γ), υπολογίστε την ισοδύναμη δύναμη

Αυτή η δύναμη εφαρμόζεται στο κέντρο βάρους της περιοχής που περιορίζεται πάνω από τη δοκό ΑΒγραμμή q(x).

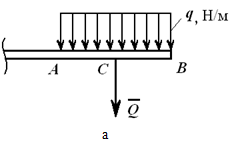
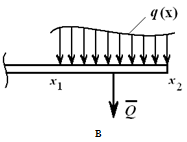
Εικόνα 1.23

Ένα παράδειγμα είναι ο υπολογισμός των δυνάμεων που σπάζουν τα τοιχώματα ενός κυλίνδρου συμπιεσμένου αερίου. Ας προσδιορίσουμε την προκύπτουσα δύναμη πίεσης στον τομέα του σωλήνα σε ένταση q[N/m]; R– ακτίνα σωλήνα, 2α– κεντρική γωνία, άξονας Βόδι– άξονας συμμετρίας (Εικόνα 1.24).

Επιλέξτε το στοιχείο τομέα με τη γωνία ∆φ και καθορίστε τη δύναμη ∆Q, που ενεργεί σε επίπεδο στοιχείο του τόξου:

∆Q = q ∙ ∆l = q ∙ R ∙ ∆φ. (1.14)

Εικόνα 1.24

Βόδιθα

∆Q x = q ∙ R ∙ ∆φ∙ cosφ. (1.15)

Λόγω της συμμετρίας του στοιχείου σωλήνα (με τόξο ΑΒ) σε σχέση με τον άξονα Βόδιπροβολή της δύναμης που προκύπτει στον άξονα Oy:

Q y = 0, δηλ. Q = Q x, (1.16)

Οπου ΑΒ- μια χορδή που συσπά τα άκρα του τόξου.

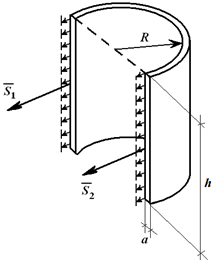
Για κυλινδρικό δοχείο με ύψος ηκαι εσωτερική πίεση Ποι τοίχοι υπόκεινται σε ένα φορτίο έντασης q = p [N/m, 2]. Εάν ο κύλινδρος κόβεται κατά μήκος της διαμέτρου (Εικόνα 1.25), τότε ισούται με F = q ∙ d ∙ h (ρε– εσωτερική διάμετρος) ή

F = p ∙ 2R ∙ h.

Δυνάμεις που σπάζουν τον κύλινδρο κατά μήκος της διαμέτρου του:

S 1 = S 2 = S;
2S = F;
S = p∙h∙R. (1.18)

Στους μηχανικούς υπολογισμούς συναντά κανείς συχνά φορτία που κατανέμονται κατά μήκος μιας δεδομένης επιφάνειας σύμφωνα με τον έναν ή τον άλλο νόμο. Ας εξετάσουμε μερικά απλά παραδείγματα κατανεμημένων δυνάμεων που βρίσκονται στο ίδιο επίπεδο.

Ένα επίπεδο σύστημα κατανεμημένων δυνάμεων χαρακτηρίζεται από την έντασή του q, δηλαδή την τιμή της δύναμης ανά μονάδα μήκους του φορτισμένου τμήματος. Η ένταση μετριέται σε Newton διαιρούμενο με μέτρα

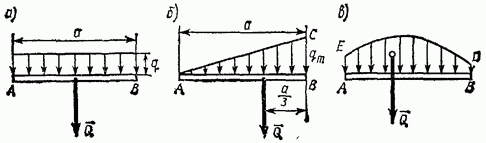
1) Δυνάμεις ομοιόμορφα κατανεμημένες κατά μήκος ενός ευθύγραμμου τμήματος (Εικ. 69, α). Για ένα τέτοιο σύστημα δυνάμεων, η ένταση q έχει σταθερή τιμή. Στους στατικούς υπολογισμούς, αυτό το σύστημα δυνάμεων μπορεί να αντικατασταθεί από το προκύπτον

Modulo,

Η δύναμη Q εφαρμόζεται στο μέσο του τμήματος ΑΒ.

2) Δυνάμεις που κατανέμονται κατά μήκος ενός ευθύγραμμου τμήματος σύμφωνα με έναν γραμμικό νόμο (Εικ. 69, β). Ένα παράδειγμα τέτοιου φορτίου μπορεί να είναι οι δυνάμεις της πίεσης του νερού σε ένα φράγμα, έχοντας υψηλότερη τιμήστο βυθό και πέφτοντας στο μηδέν στην επιφάνεια του νερού. Για αυτές τις δυνάμεις, η ένταση q είναι το μέγεθος της μεταβλητής, που αυξάνεται από το μηδέν στη μέγιστη τιμή.Το προκύπτον Q τέτοιων δυνάμεων προσδιορίζεται παρόμοια με το αποτέλεσμα των δυνάμεων βαρύτητας που δρουν σε μια ομοιογενή τριγωνική πλάκα ABC. Εφόσον το βάρος μιας ομοιογενούς πλάκας είναι ανάλογο με το εμβαδόν της, τότε, modulo,

Η δύναμη Q εφαρμόζεται σε απόσταση από την πλευρά BC του τριγώνου ABC (βλ. § 35, παράγραφος 2).

3) Δυνάμεις που κατανέμονται κατά μήκος ενός ευθύγραμμου τμήματος σύμφωνα με έναν αυθαίρετο νόμο (Εικ. 69, γ). Το προκύπτον Q τέτοιων δυνάμεων, κατ' αναλογία με τη δύναμη βαρύτητας, είναι ίσο σε μέγεθος με το εμβαδόν του σχήματος ΑΒΔΕ, μετρημένο στην κατάλληλη κλίμακα και διέρχεται από το κέντρο βάρους αυτής της περιοχής (το θέμα του προσδιορισμού τα κέντρα βάρους των περιοχών θα συζητηθούν στην § 33).

4) Δυνάμεις ομοιόμορφα κατανεμημένες κατά μήκος του τόξου ενός κύκλου (Εικ. 70). Ένα παράδειγμα τέτοιων δυνάμεων είναι οι δυνάμεις της υδροστατικής πίεσης στα πλευρικά τοιχώματα ενός κυλινδρικού δοχείου.

Έστω η ακτίνα του τόξου ίση με , πού είναι ο άξονας συμμετρίας κατά μήκος του οποίου κατευθύνουμε τον άξονα.

Για να προσδιορίσουμε την τιμή του Q, επιλέγουμε ένα στοιχείο στο τόξο, η θέση του οποίου καθορίζεται από τη γωνία και το μήκος της δύναμης που ασκεί αυτό το στοιχείο είναι αριθμητικά ίσο και η προβολή αυτής της δύναμης στον άξονα θα είναι τότε

Αλλά από το Σχ. 70 είναι σαφές ότι Επομένως, έκτοτε

πού είναι το μήκος της χορδής που υποτάσσει το τόξο ΑΒ; q - ένταση.

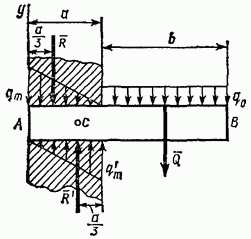
Πρόβλημα 27. Ένα ομοιόμορφα κατανεμημένο φορτίο έντασης δρα σε μια δοκό προβόλου Α Β, οι διαστάσεις της οποίας φαίνονται στο σχέδιο (Εικ. 71). Παραβλέποντας το βάρος της δοκού και υποθέτοντας ότι οι δυνάμεις πίεσης στο ενσωματωμένο άκρο καθορίζονται σύμφωνα με σε έναν γραμμικό νόμο, προσδιορίστε τις τιμές των υψηλότερων εντάσεων αυτών των δυνάμεων, Αν

Λύση. Αντικαθιστούμε κατανεμημένες δυνάμειςτα προκύπτοντα Q, R και R, όπου σύμφωνα με τους τύπους (35) και (36)

και να δημιουργήσετε συνθήκες ισορροπίας (33) για παράλληλες δυνάμεις που ασκούν τη δοκό

Αντικαθιστώντας εδώ αντί των Q, R και R τις τιμές τους και λύνοντας τις εξισώσεις που προκύπτουν, θα βρούμε τελικά

Για παράδειγμα, πότε παίρνουμε και πότε

Πρόβλημα 28. Ένας κυλινδρικός κύλινδρος του οποίου το ύψος είναι H και η εσωτερική διάμετρος d, γεμίζεται με αέριο υπό πίεση Το πάχος των κυλινδρικών τοιχωμάτων του κυλίνδρου είναι α. Προσδιορίστε τις εφελκυστικές τάσεις που αντιμετωπίζουν αυτοί οι τοίχοι στις κατευθύνσεις: 1) διαμήκεις και 2) εγκάρσιες (η τάση είναι ίση με τον λόγο της δύναμης εφελκυσμού προς το εμβαδόν της διατομής), θεωρώντας την μικρή.

Λύση. 1) Ας κόψουμε τον κύλινδρο σε δύο μέρη με ένα επίπεδο κάθετο στον άξονά του και ας εξετάσουμε την ισορροπία ενός από αυτά (Εικ.

72, α). Ασκείται προς την κατεύθυνση του άξονα του κυλίνδρου από τη δύναμη πίεσης στον πυθμένα και τις δυνάμεις που κατανέμονται στην περιοχή της διατομής (η δράση του απορριφθέντος μισού), το αποτέλεσμα των οποίων θα συμβολίζεται με Q. Σε ισορροπία

Η απόσταση μεταξύ των συγκεντρωμένων φορτίων είναι η ίδια και η απόσταση από την αρχή του ανοίγματος έως το πρώτο συγκεντρωμένο φορτίο είναι ίση με την απόσταση μεταξύ των συγκεντρωμένων φορτίων. Σε αυτήν την περίπτωση, συγκεντρωμένα φορτία πέφτουν επίσης στην αρχή και στο τέλος του ανοίγματος, αλλά ταυτόχρονα προκαλούν μόνο αύξηση αντίδραση εδάφους, τα ακραία συγκεντρωμένα φορτία δεν επηρεάζουν με κανέναν τρόπο την τιμή των ροπών κάμψης και της παραμόρφωσης και επομένως κατά τον υπολογισμό φέρουσα ικανότηταδομές δεν λαμβάνονται υπόψη. Ας το εξετάσουμε χρησιμοποιώντας το παράδειγμα των δοκών δαπέδου που στηρίζονται σε ένα υπέρθυρο. Τούβλο, που μπορεί να βρίσκεται ανάμεσα στο υπέρθυρο και τις δοκούς του δαπέδου, και ταυτόχρονα να δημιουργεί ένα ομοιόμορφα κατανεμημένο φορτίο, δεν εμφανίζεται για ευκολία αντίληψης.

Εικόνα 1. Μείωση των συγκεντρωμένων φορτίων σε ισοδύναμο ομοιόμορφα κατανεμημένο φορτίο.

Όπως φαίνεται από το σχήμα 1, η καθοριστική ροπή είναι η ροπή κάμψης, η οποία χρησιμοποιείται στους υπολογισμούς αντοχής των κατασκευών. Έτσι, για να παράγει ένα ομοιόμορφα κατανεμημένο φορτίο την ίδια ροπή κάμψης με ένα συγκεντρωμένο φορτίο, πρέπει να πολλαπλασιαστεί με τον κατάλληλο συντελεστή μετάβασης (συντελεστής ισοδυναμίας). Και αυτός ο συντελεστής καθορίζεται από τις συνθήκες ισότητας των ροπών. Νομίζω ότι το Σχήμα 1 το απεικονίζει πολύ καλά. Και αναλύοντας τις εξαρτήσεις που αποκτήθηκαν, μπορείτε να εξαγάγετε έναν γενικό τύπο για τον προσδιορισμό του συντελεστή μετάβασης. Έτσι, εάν ο αριθμός των εφαρμοζόμενων συγκεντρωτικών φορτίων είναι περιττός, π.χ. ένα από τα συγκεντρωμένα φορτία πέφτει αναγκαστικά στο μέσο του ανοίγματος, τότε για να προσδιορίσετε τον συντελεστή ισοδυναμίας μπορείτε να χρησιμοποιήσετε τον τύπο:

γ = n/(n - 1) (305.1.1)

όπου n είναι ο αριθμός των ανοιγμάτων μεταξύ συγκεντρωμένων φορτίων.

q eq = γ(n-1)Q/l (305.1.2)

όπου (n-1) είναι ο αριθμός των συγκεντρωμένων φορτίων.

Ωστόσο, μερικές φορές είναι πιο βολικό να κάνετε υπολογισμούς με βάση τον αριθμό των συγκεντρωμένων φορτίων. Αν αυτή η ποσότητα εκφράζεται με τη μεταβλητή m, τότε

γ = (m +1)/m (305.1.3)

Στην περίπτωση αυτή, το ισοδύναμο ομοιόμορφα κατανεμημένο φορτίο θα είναι ίσο με:

q eq = γmQ/l (305.1.4)

Όταν ο αριθμός των συγκεντρωμένων φορτίων είναι άρτιος, δηλ. κανένα από τα συγκεντρωμένα φορτία δεν πέφτει στο μέσο του ανοίγματος, τότε η τιμή του συντελεστή μπορεί να ληφθεί ως η επόμενη περιττή τιμή του αριθμού των συγκεντρωμένων φορτίων. Γενικά, με την επιφύλαξη των καθορισμένων συνθηκών φόρτωσης, μπορούν να γίνουν δεκτοί οι ακόλουθοι συντελεστές μετάβασης:

γ = 2- εάν η υπό εξέταση κατασκευή, για παράδειγμα, η δοκός δέχεται μόνο ένα συγκεντρωμένο φορτίο στη μέση του ανωφρίου.

γ = 1,33- για δοκό που υπόκειται σε 2 ή 3 συγκεντρωμένα φορτία.

γ = 1,2- για δοκό που υπόκειται σε 4 ή 5 συγκεντρωμένα φορτία.

γ = 1,142- για δοκό που υπόκειται σε 6 ή 7 συγκεντρωμένα φορτία.

γ = 1,11- για δοκό που υπόκειται σε 8 ή 9 συγκεντρωμένα φορτία.

Επιλογή 2

Η απόσταση μεταξύ των συγκεντρωμένων φορτίων είναι η ίδια, με την απόσταση από την αρχή του ανοίγματος έως το πρώτο συγκεντρωμένο φορτίο να είναι ίση με το ήμισυ της απόστασης μεταξύ των συγκεντρωμένων φορτίων. Σε αυτή την περίπτωση, τα συγκεντρωμένα φορτία δεν πέφτουν στην αρχή και στο τέλος του ανοίγματος.

Σχήμα 2. Τιμές συντελεστών μετάβασης για την επιλογή 2 εφαρμογής συγκεντρωμένων φορτίων.

Όπως φαίνεται από το Σχήμα 2, με αυτήν την επιλογή φόρτωσης, η τιμή του συντελεστή μετάβασης θα είναι σημαντικά μικρότερη. Έτσι, για παράδειγμα, με ζυγό αριθμό συγκεντρωμένων φορτίων, ο συντελεστής μετάβασης μπορεί γενικά να ληφθεί ίσος με τη μονάδα. Για έναν περιττό αριθμό συγκεντρωμένων φορτίων, ο τύπος μπορεί να χρησιμοποιηθεί για τον προσδιορισμό του συντελεστή ισοδυναμίας:

γ = (m +7)/(m +6) (305.2.1)

όπου m είναι ο αριθμός των συγκεντρωμένων φορτίων.

Σε αυτήν την περίπτωση, το ισοδύναμο ομοιόμορφα κατανεμημένο φορτίο θα εξακολουθεί να είναι ίσο με:

q eq = γmQ/l (305.1.4)

Γενικά, με την επιφύλαξη των καθορισμένων συνθηκών φόρτωσης, μπορούν να γίνουν δεκτοί οι ακόλουθοι συντελεστές μετάβασης:

γ = 2- εάν η υπό εξέταση κατασκευή, για παράδειγμα, υπόκειται σε ένα μόνο συγκεντρωμένο φορτίο στη μέση του ανώφλι και εάν οι δοκοί δαπέδου πέφτουν στην αρχή ή στο τέλος του ανοίγματος ή βρίσκονται αυθαίρετα μακριά από την αρχή και το τέλος του εύρος, σε αυτή η υπόθεσηδεν έχει σημασία. Και αυτό είναι σημαντικό κατά τον προσδιορισμό του συγκεντρωμένου φορτίου.

γ = 1- εάν η εν λόγω κατασκευή υπόκειται σε ζυγό αριθμό φορτίων.

γ = 1,11- για δοκό που υπόκειται σε 3 συγκεντρωμένα φορτία.

γ = 1,091- για δοκό που υπόκειται σε 5 συγκεντρωμένα φορτία.

γ = 1,076- για δοκό που υπόκειται σε 7 συγκεντρωμένα φορτία.

γ = 1,067- για δοκό που υπόκειται σε 9 συγκεντρωμένα φορτία.

Παρά ορισμένους περίπλοκους ορισμούς, οι συντελεστές ισοδυναμίας είναι πολύ απλοί και βολικοί. Δεδομένου ότι κατά τους υπολογισμούς το κατανεμημένο φορτίο που ενεργεί ανά τετραγωνικό ή γραμμικό μέτρο είναι πολύ συχνά γνωστό, για να μην μετατραπεί το κατανεμημένο φορτίο πρώτα σε συγκεντρωμένο και μετά πάλι σε ισοδύναμο κατανεμημένο, αρκεί απλώς να πολλαπλασιαστεί η τιμή του κατανεμημένο φορτίο με τον κατάλληλο συντελεστή. Για παράδειγμα, η οροφή θα υπόκειται σε τυπικό κατανεμημένο φορτίο 400 kg/m2, ενώ το νεκρό βάρος της οροφής θα είναι άλλα 300 kg/m2. Στη συνέχεια, με μήκος δοκού δαπέδου 6 m, ένα ομοιόμορφα κατανεμημένο φορτίο q = 6(400 + 300)/2 = 2100 kg/m θα μπορούσε να δράσει στο υπέρθυρο. Και τότε, εάν υπάρχει μόνο μία δοκός δαπέδου στο μέσο του ανοίγματος, τότε γ = 2, και

q eq = γq = 2q (305.2.2)

Εάν καμία από τις δύο παραπάνω προϋποθέσεις δεν πληρούται, τότε είναι αδύνατο να χρησιμοποιηθούν συντελεστές μετάβασης στην καθαρή τους μορφή· πρέπει να προσθέσετε δύο επιπλέον συντελεστές που λαμβάνουν υπόψη την απόσταση από τις δοκούς που δεν πέφτουν στην αρχή και στο τέλος του ανοίγματος του υπέρθυρου, καθώς και της πιθανής ασυμμετρίας της εφαρμογής συγκεντρωμένων φορτίων. Κατ' αρχήν, είναι δυνατόν να εξαχθούν τέτοιοι συντελεστές, αλλά σε κάθε περίπτωση θα είναι μειωμένοι σε όλες τις περιπτώσεις εάν λάβουμε υπόψη την 1η περίπτωση φόρτισης και στο 50% των περιπτώσεων εάν λάβουμε υπόψη τη 2η περίπτωση φορτίου, δηλ. οι τιμές τέτοιων συντελεστών θα είναι< 1. А потому для упрощения расчетов, а заодно и для большего запаса по прочности рассчитываемой конструкции вполне хватит коэффициентов, приведенных при первых двух вариантах загружения.