荷重が不均一に分散されています。 分散荷重

表面力と体積力は、特定の表面または体積に分布する荷重を表します。 このような荷重は強度によって与えられます。強度とは、ある体積、ある面積、またはある長さの単位あたりの力です。

多くの実際に興味深い問題を解決する上で特別な役割を占めるのは、特定の梁の法線に沿って適用される平坦な分布荷重の場合です。 軸がビームに沿って向いている場合 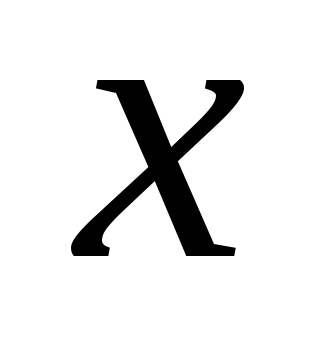の場合、強度は座標の関数になります。 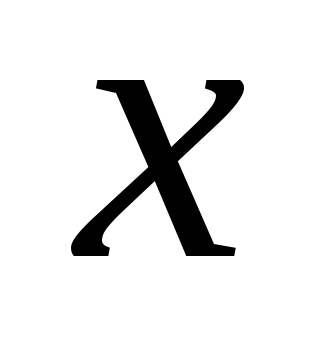N/m で測定されます。 強度は単位長さあたりの力を表します。

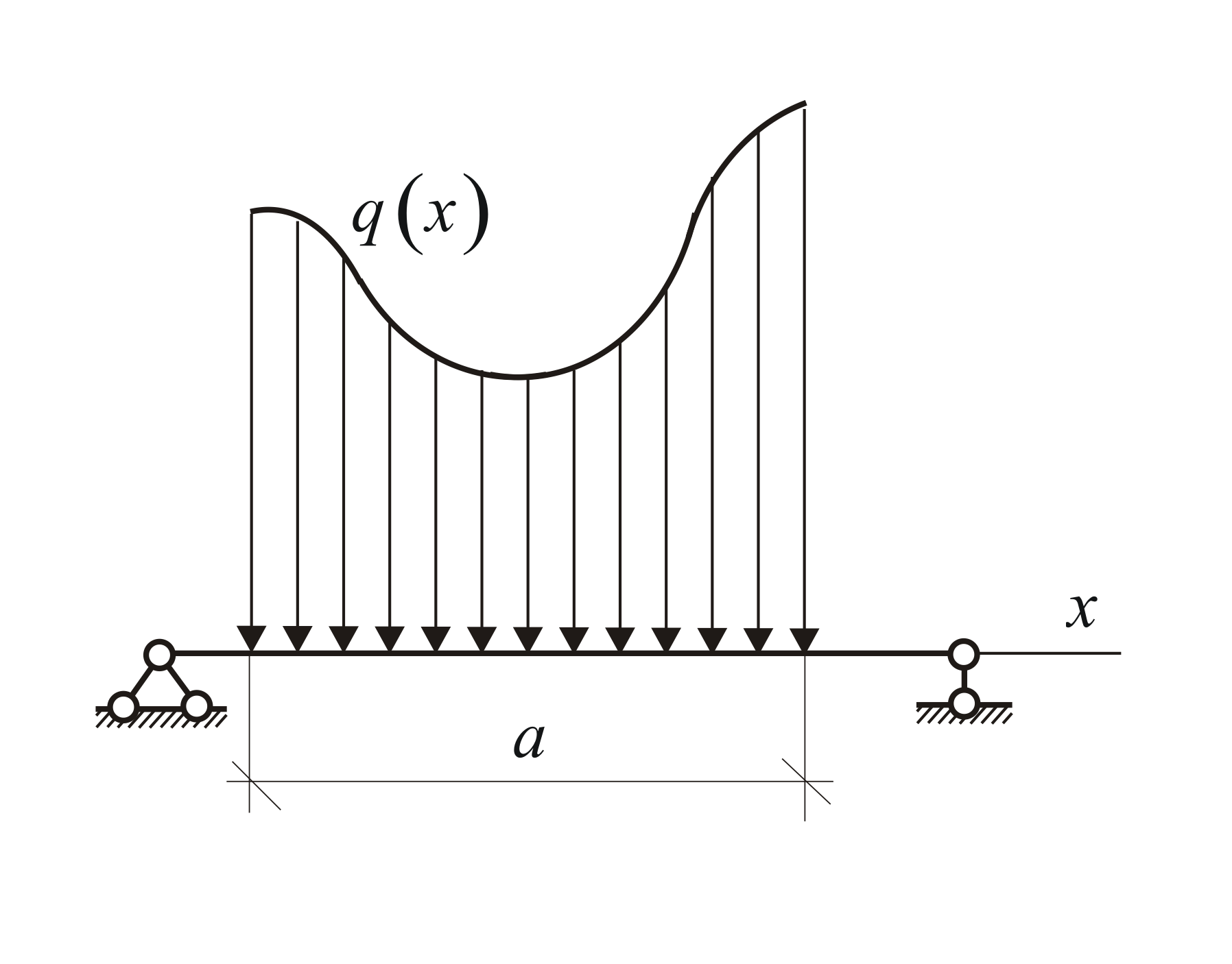
梁で囲まれた平面図と荷重強度グラフを分布荷重図といいます（図1.28）。 解決する問題の性質により、変形を無視できる場合、つまり、 物体は絶対的に剛体であると考えることができるため、分散荷重は合力によって置き換えることができます (またそうすべきです)。

ビームを分割しましょう 長さ

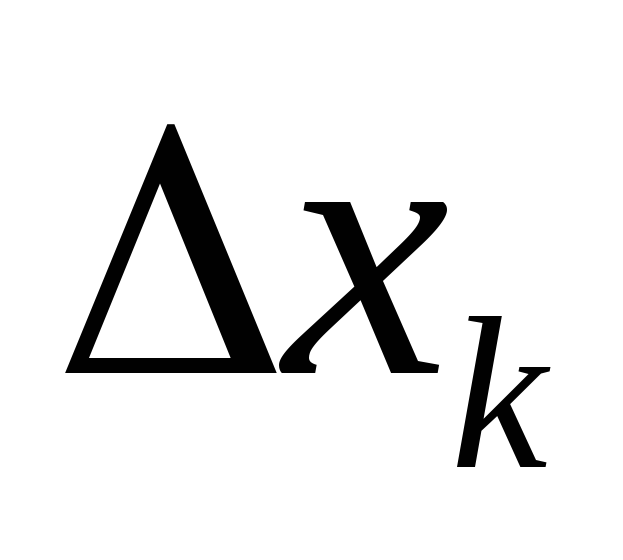、それぞれの強度が一定で等しいと仮定します。

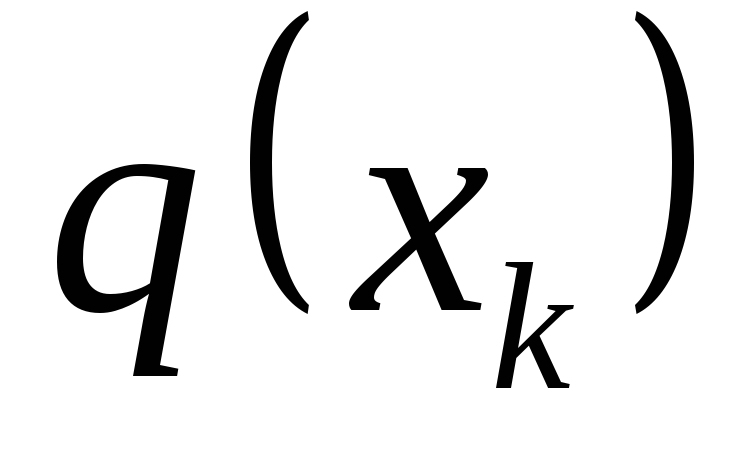、 どこ 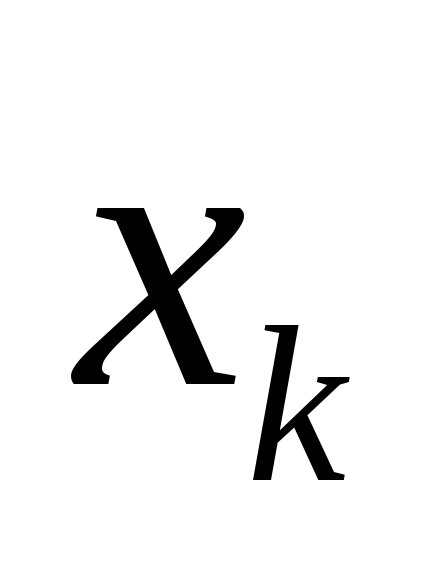– セグメントの座標

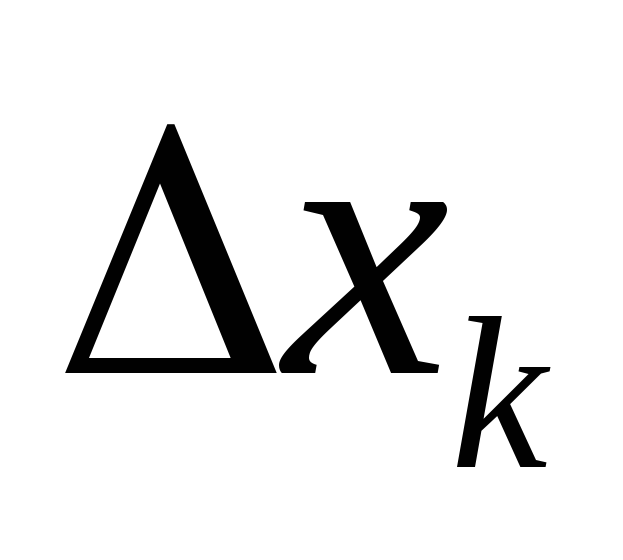。 この場合、強度曲線は破線に置き換えられ、セグメントごとの荷重が表示されます。

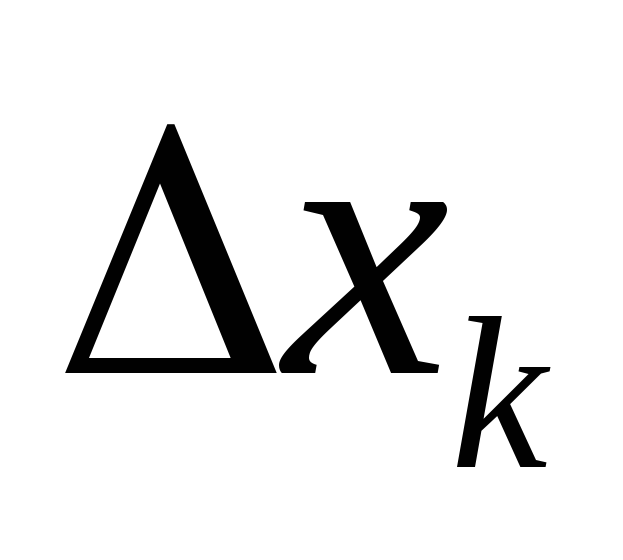、集中力に置き換えられます

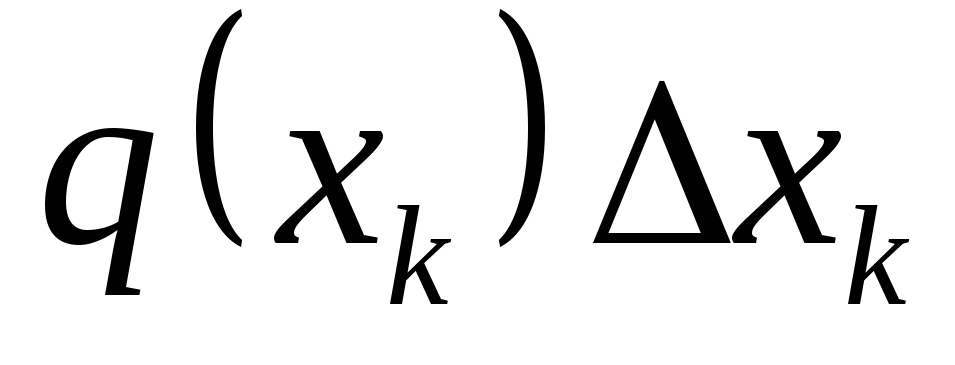、ポイントで適用されます 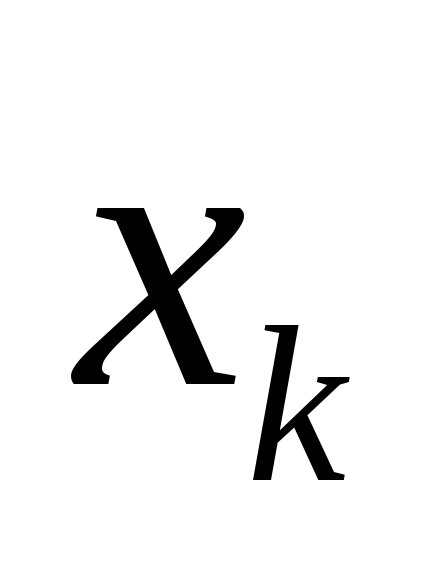(図1.29)。 結果として生じる平行力のシステムは、各セグメントに作用し、平行力の中心に加えられる力の合計に等しい合力を持ちます。

セグメントが小さいほど、このような表現が実際の状況をより正確に表すことは明らかです。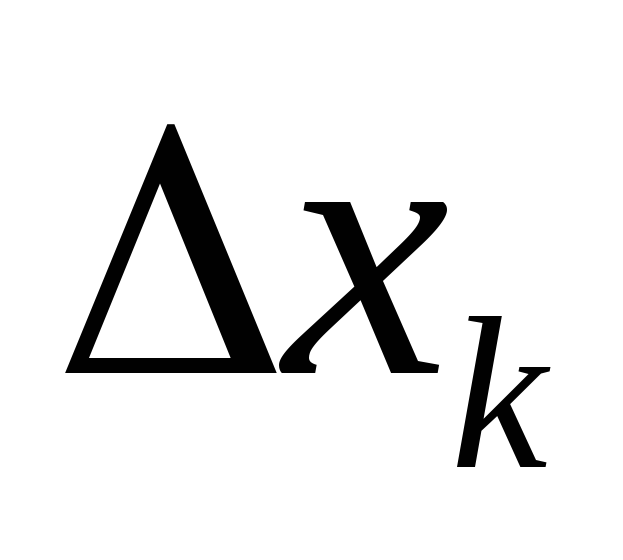

、つまり セグメントの数が増えるほど 。 セグメントの長さの限界まで通過することで正確な結果が得られます。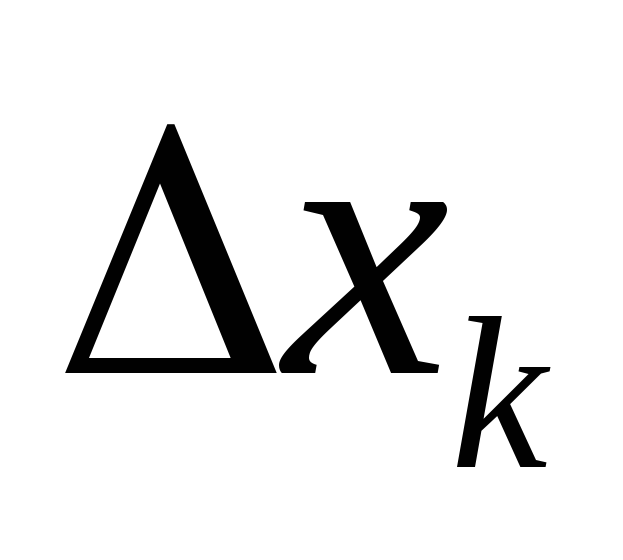

ゼロに向かう傾向にあります。 説明した手順の結果として得られる極限は積分です。 したがって、結果の係数については次のようになります。

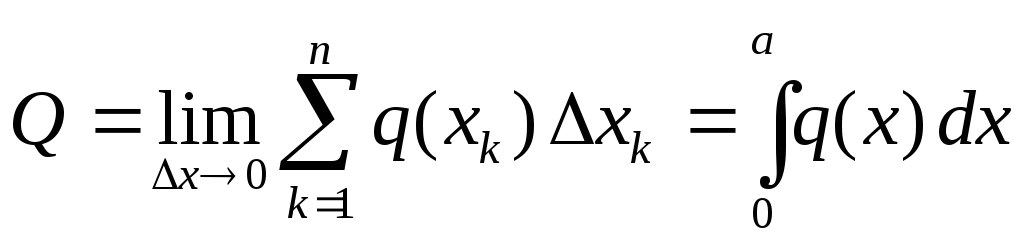
点の座標を決定するには 結果を応用してバリニョンの定理を使用します。

力の系に合力がある場合、任意の中心 (任意の軸) に対する合力のモーメントは、この中心 (この軸) に対するシステムのすべての力のモーメントの合計に等しくなります。

力の系に関するこの定理を書く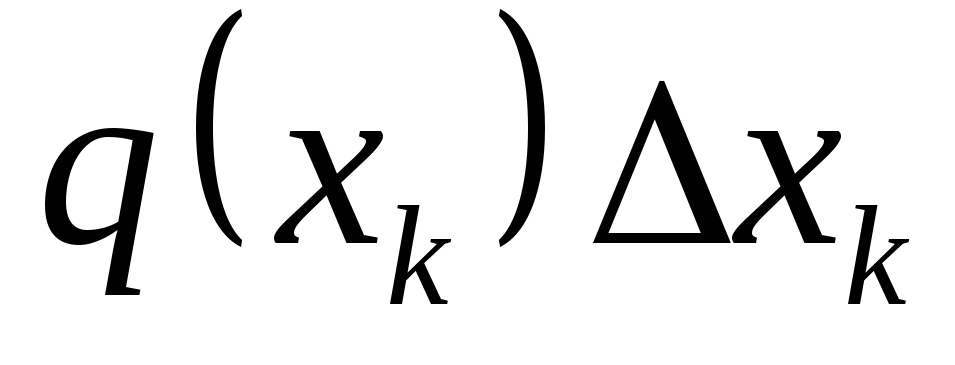

軸上の投影で 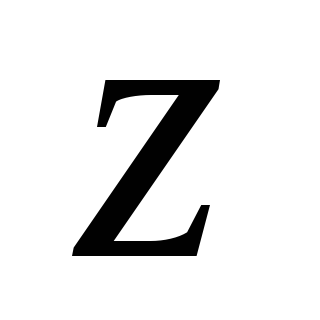そして、セグメントの長さがゼロになる傾向にある限界まで渡すと、次の結果が得られます。

明らかに、結果のモジュールは分布荷重図の面積に数値的に等しく、その適用点は分布荷重図の形状を有する均質な板の重心と一致します。

よく発生する 2 つのケースに注目してみましょう。

,

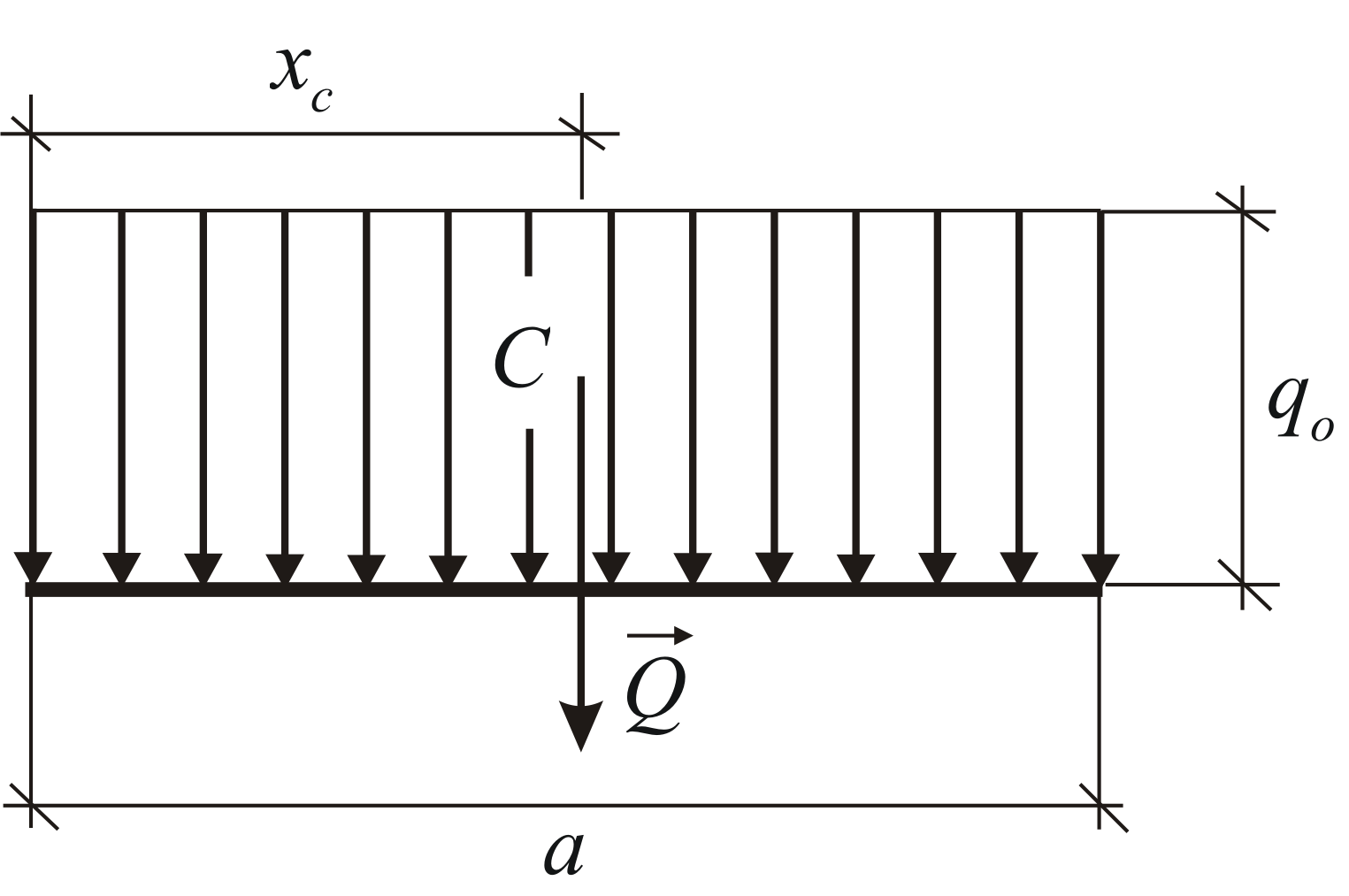
(図1.30)。 結果のモジュールとその適用点の座標は、次の式で決定されます。

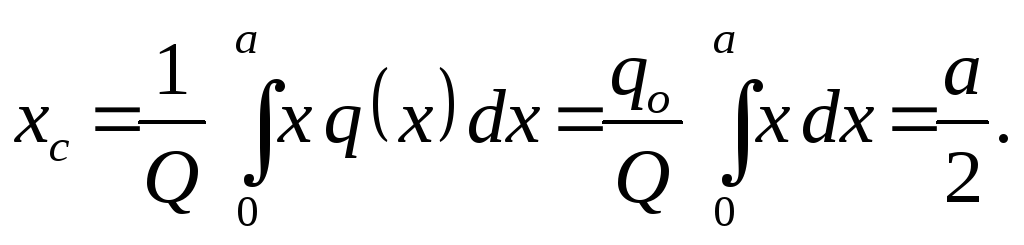
エンジニアリングの現場では、このような負荷が頻繁に発生します。 ほとんどの場合、重量と風荷重は均一に分布していると考えられます。

,

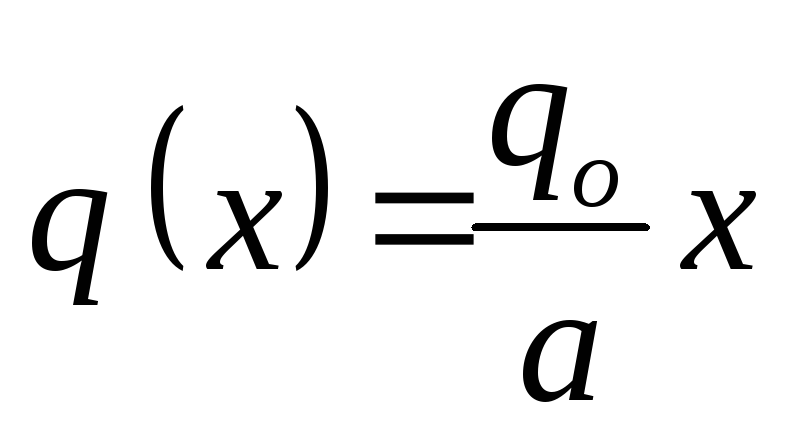(図1.31)。 この場合：

特に、垂直の壁にかかる水圧は深さに正比例します。 .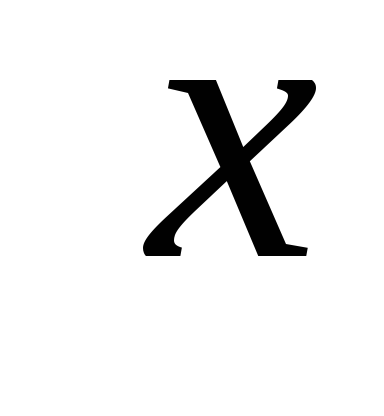

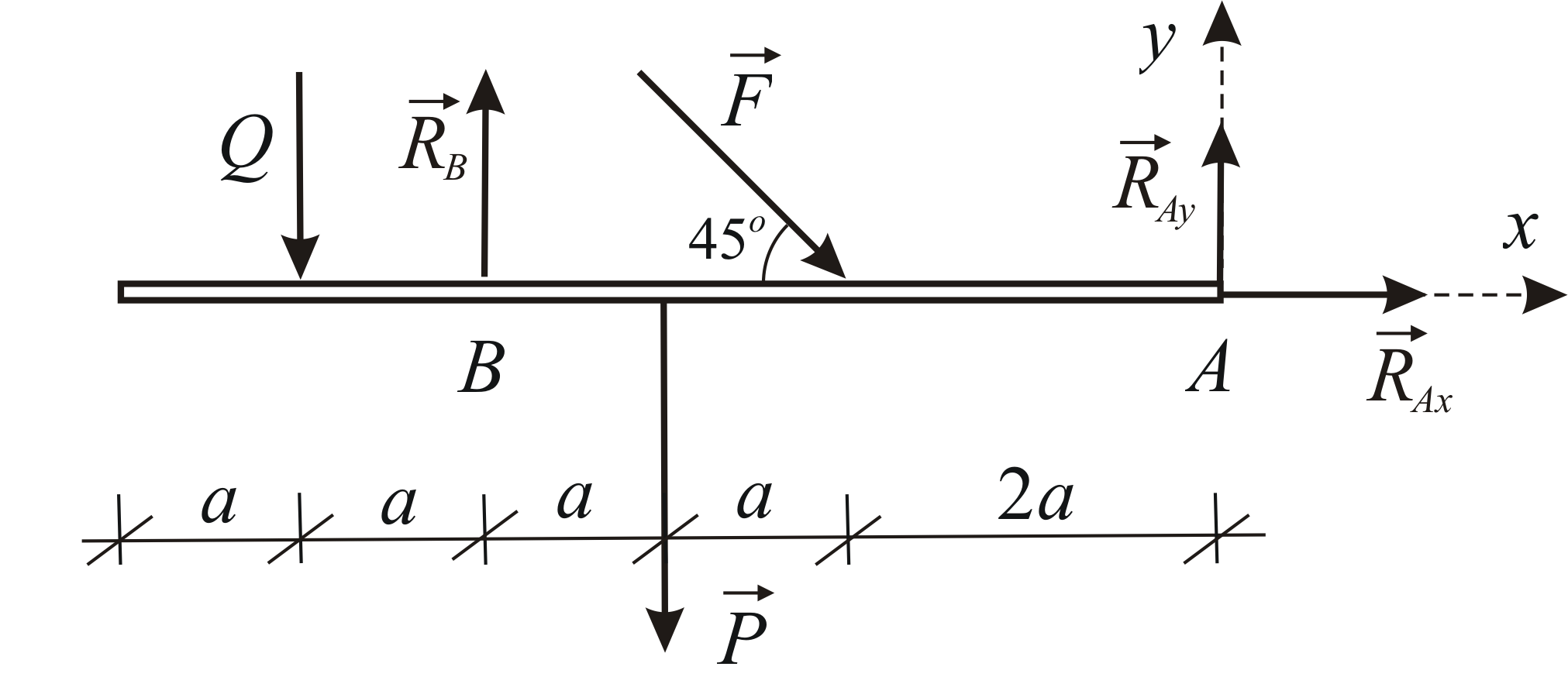
例1.5

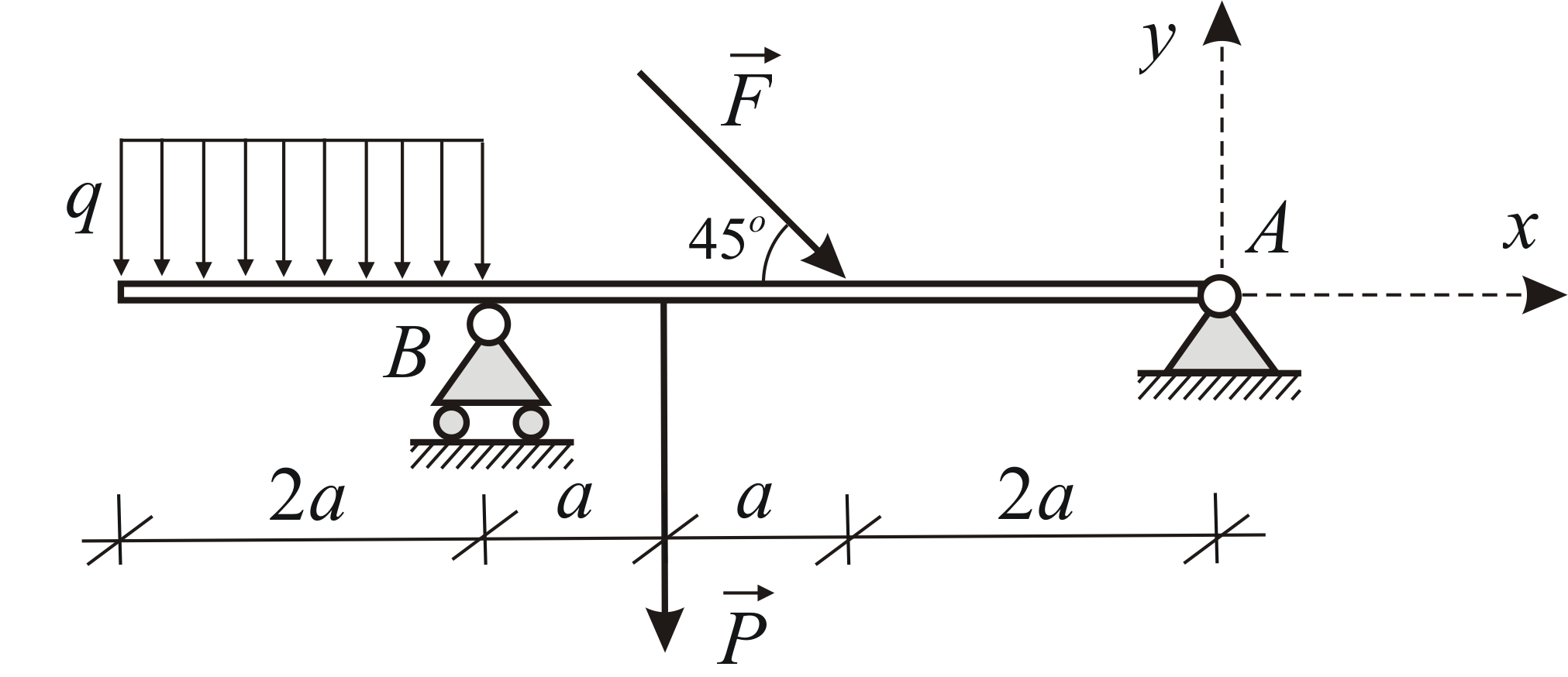
支持反応を決定する そして 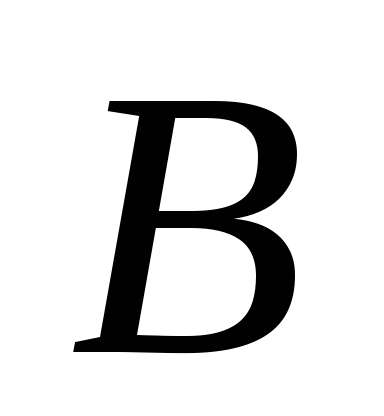ビームには 2 つの集中した力と均一に分散された荷重が作用します。 与えられる:

分布荷重の結果を求めてみましょう。 結果の係数は以下に等しい

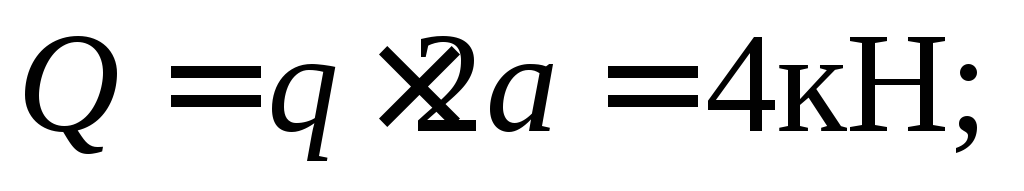
肩の強さ 点に対して 等しい

梁の平衡を考えてみましょう。 電源回路を図に示します。 1.33。

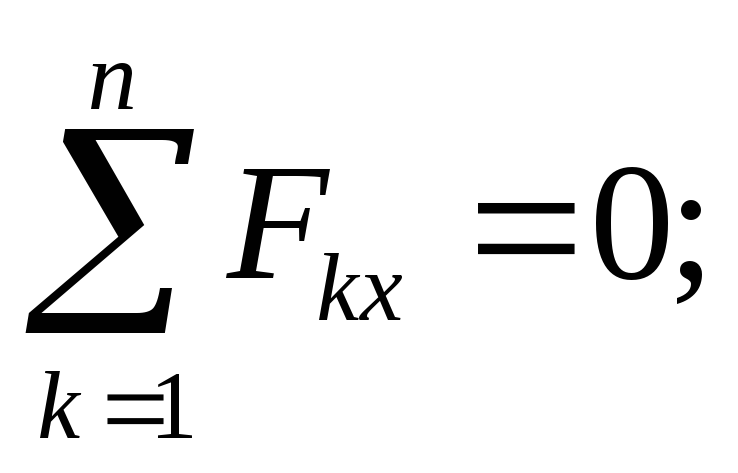
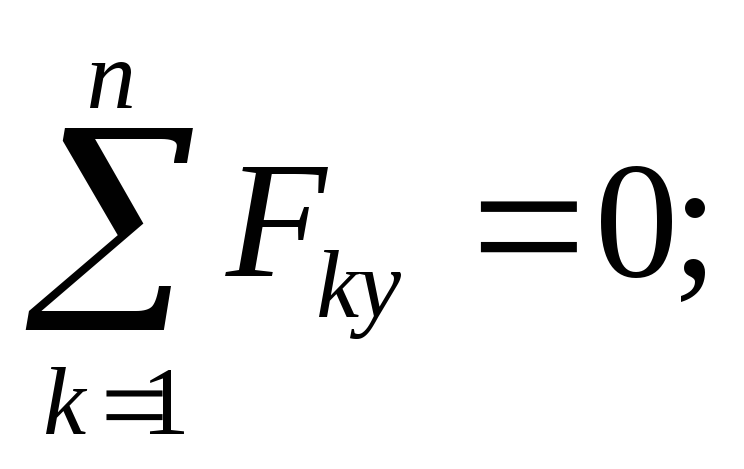
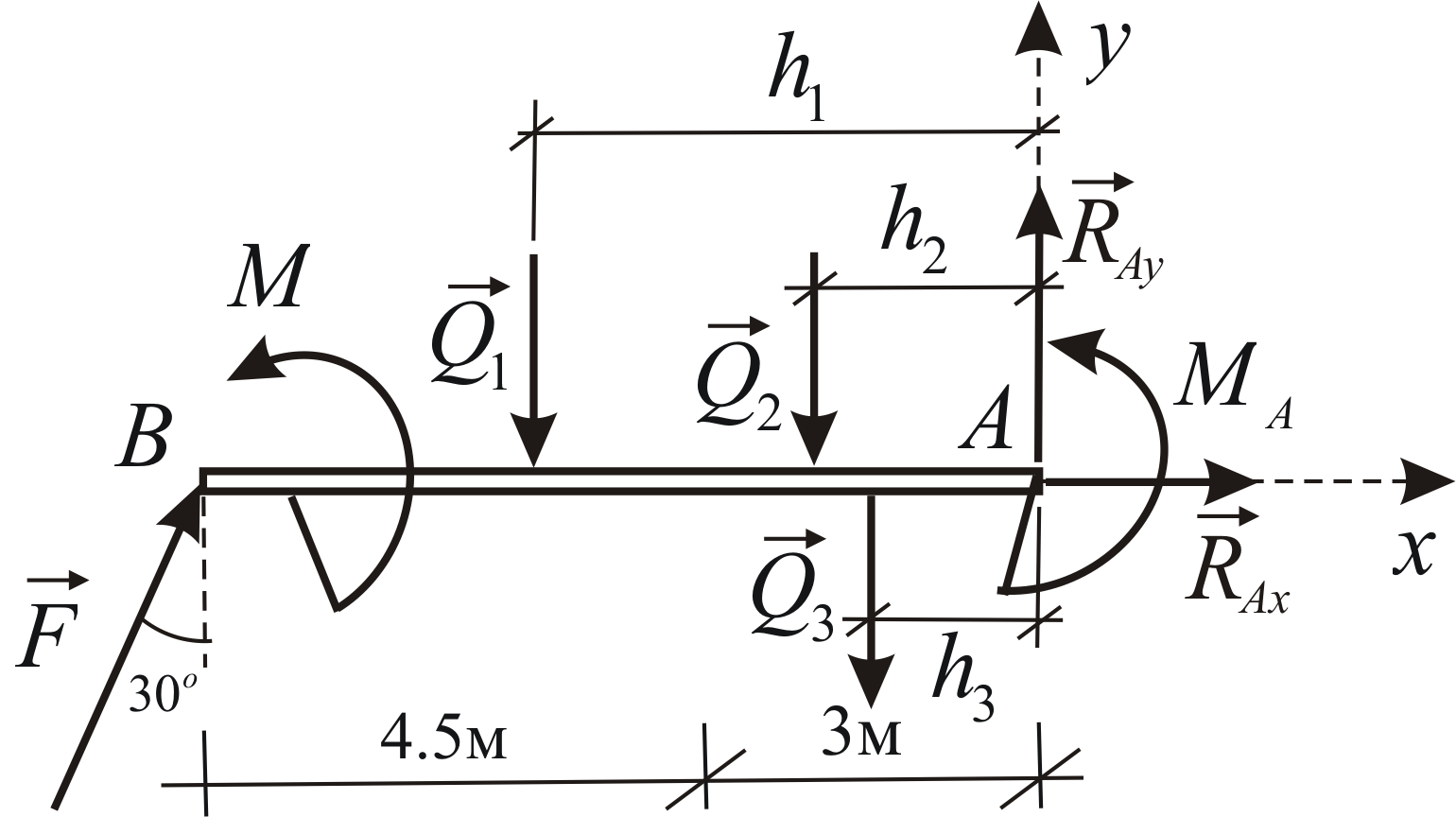
例1.6

集中力、一対の力、および分散荷重の作用下での片持ち梁の埋め込みの反力を求めます (図 1.34)。

分散荷重を 3 つの集中力に置き換えてみましょう。 これを行うには、分布荷重の図を 2 つの三角形と 1 つの長方形に分割します。 我々は気づく

電源回路を図に示します。 1.35。

軸に対する合算物の腕を計算しましょう

検討中のケースの平衡条件は次の形式になります。

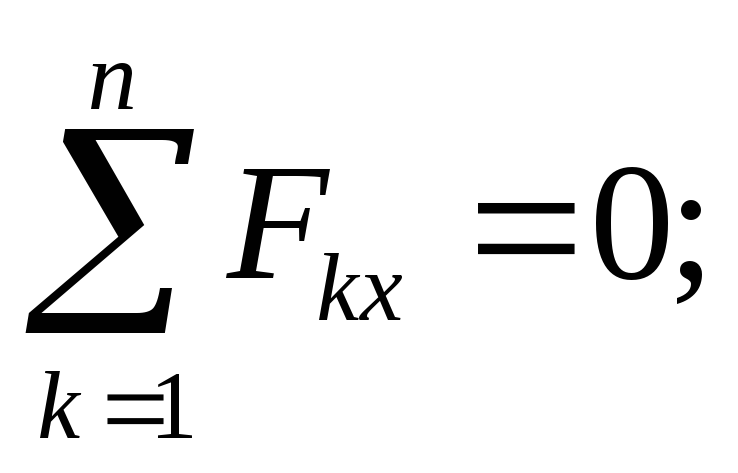
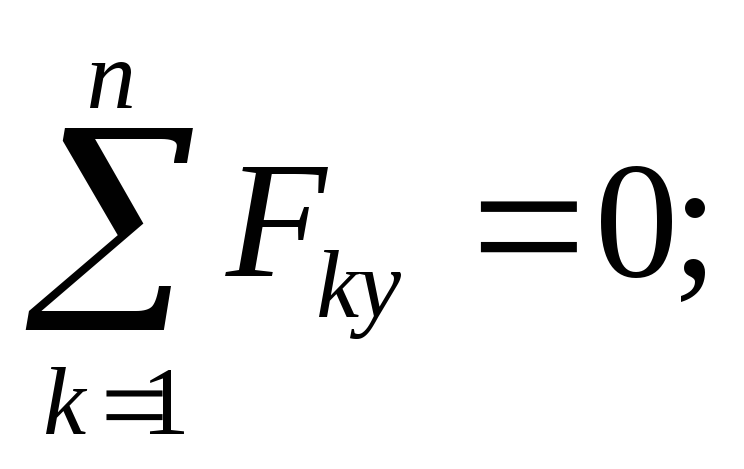
セルフチェックのための質問:

1. 分布荷重強度とは何ですか?

2. 結果として生じる分布荷重の係数を計算するにはどうすればよいですか?

3. 分散結果の適用点の座標を計算する方法

負荷？

4. 係数とは何ですか?また、等分布荷重の作用点の座標は何ですか?

5. 線形分布荷重の作用点の係数と座標は何ですか?

I.V. Meshchersky による問題集より: 4.28; 4.29; 4.30; 4.33; 4.34。

教科書「理論力学 - 理論と実践」より: SR-2 キット。 SR-3。

実践レッスンNo.4～5

分散荷重

機構の部品、構造、要素への影響は、分散荷重によって指定できます。 フラットシステムアクションの強度は、空間システム内の構造の長さに沿って、つまりエリアに沿って設定されます。

線形荷重の寸法は N/m、面積に分布する荷重の場合は N/m 2、体積荷重の場合 (たとえば、構造要素の自重を考慮する場合) - N/m 3 です。

たとえば、図 1.23 では、N/m 単位で測定された a が長さに沿って均一に分布していることが示されています。 この負荷は集中した力で置き換えることができます

Q = q ∙ AB[H]、

セグメントの途中に適用される AB.

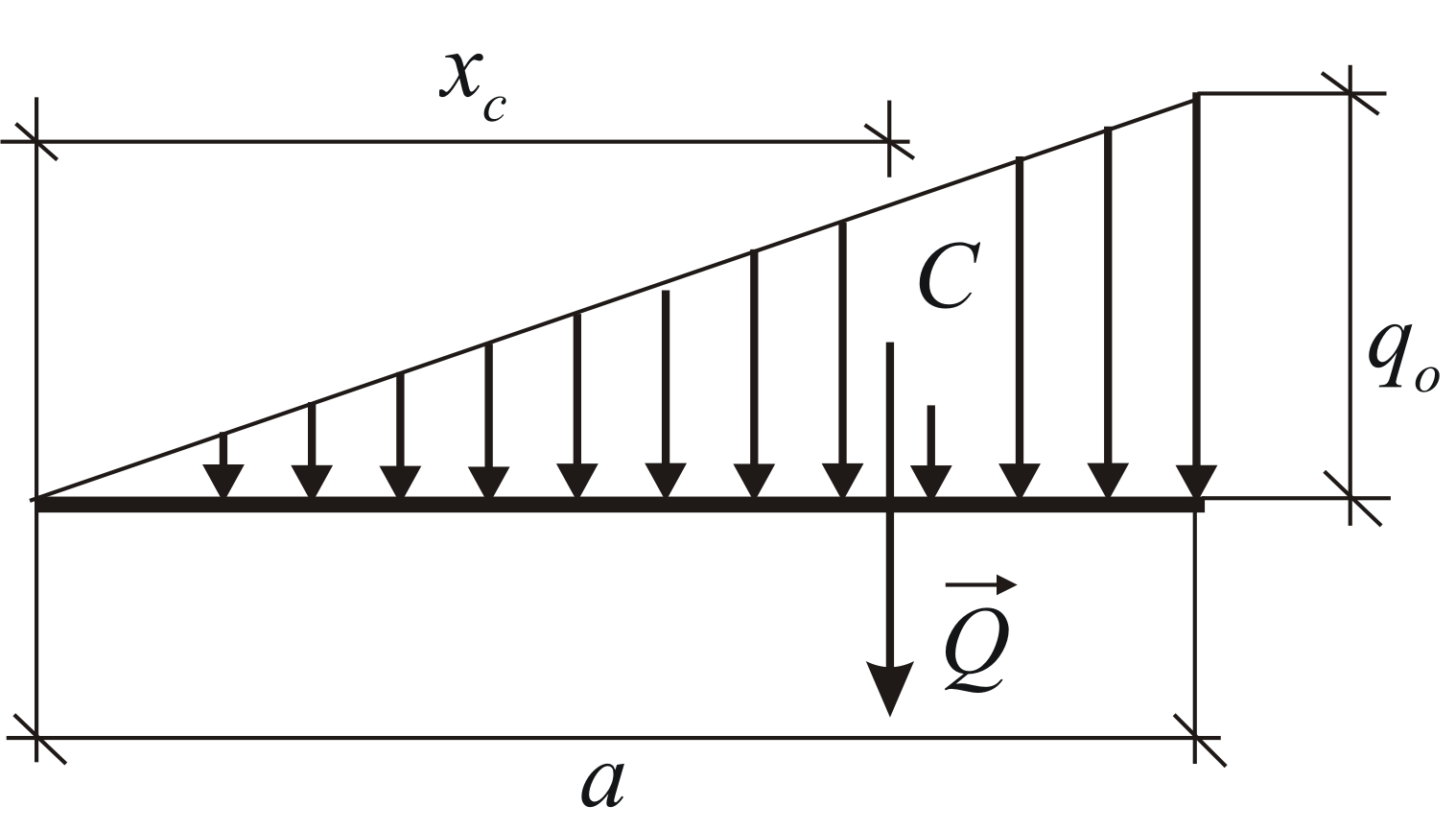
図 1.23、b は均一に減少 (増加) する荷重を示しており、これは合力で置き換えることができます。

Q = q max ∙AB/2,

ポイントで適用される C、 そして AC = 2/3AB.

任意の場合、関数を知ることで q(x)(図 1.23、c)、等価力を計算します。

この力は、ビームの上の境界領域の重心に適用されます。 ABライン q(x).

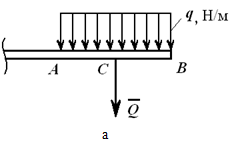
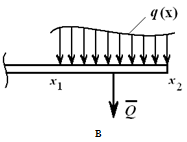
図1.23

例としては、圧縮ガスシリンダーの壁を破壊する力の計算があります。 次の強度でパイプセクターに生じる圧力を決定してみましょう。 q[N/m]; R– パイプ半径、 2α– 中心角、軸 牛- 対称軸 (図 1.24)。

角度のある扇形要素を選択しましょう ∆φ そして強さを決める ΔQ平らな円弧要素に作用する：

∆Q = q ∙ ∆l = q ∙ R ∙ ∆φ. (1.14)

図1.24

牛意思

∆Q x = q ∙ R ∙ ∆φ ∙ cosφ. (1.15)

パイプ要素の対称性（円弧を伴う）により、 AB) 軸に対して 牛結果として生じる力の軸への投影 オイ:

Qy = 0、つまり Q = Q x, (1.16)

どこ AB円弧の両端を規定する弦です。

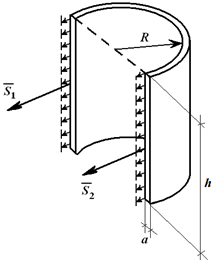
高さのある円筒形容器の場合 hそして内圧 P壁には強度が詰まっています q = p [N/m, 2]。 円柱を直径に沿って切断すると (図 1.25)、次のようになります。 F = q ∙ d ∙ h (d– 内径）または

F = p ∙ 2R ∙ h.

直径に沿ってシリンダーを破壊する力:

S 1 = S 2 = S;
2S = F;
S = p・h・R. (1.18)

工学計算では、何らかの法則に従って特定の表面に沿って荷重が分散されることがよくあります。 同じ平面内に分散された力の簡単な例をいくつか考えてみましょう。

力が分散された平坦なシステムは、その強度 q、つまり負荷がかかったセグメントの単位長さあたりの力の値によって特徴付けられます。 強度はニュートンをメートルで割った値で測定されます。

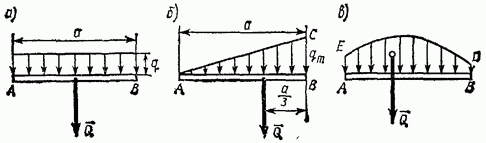
1) 直線セグメントに沿って均一に分布する力 (図 69、a)。 このような力の系では、強度 q は一定の値になります。 静的計算では、この力の系は合力によって置き換えることができます。

モジュロ、

力 Q はセグメント AB の中央に適用されます。

2) 線形法則に従って直線セグメントに沿って分布する力 (図 69、b)。 このような負荷の例としては、ダムにかかる水圧が挙げられます。 最高値底ではゼロになり、水面ではゼロになります。 これらの力の強度 q は変数の大きさであり、0 から最大値まで増加します。このような力の合力 Q は、均質な三角形の板 ABC に作用する重力の合力と同様に決定されます。 均質なプレートの重量はその面積に比例するため、法は次のようになります。

力 Q は、三角形 ABC の辺 BC から一定の距離を置いて加えられます (§ 35、段落 2 を参照)。

3) 任意の法則に従って直線セグメントに沿って分布する力 (図 69、c)。 このような力の合力 Q は、重力と類推すると、適切なスケールで測定した図の面積 ABDE に大きさが等しく、この面積の重心を通過します（決定の問題）領域の重心については § 33) で説明します。

4) 力は円弧に沿って均等に分布します (図 70)。 このような力の例としては、円筒形の容器の側壁にかかる静水圧の力が挙げられます。

円弧の半径を に等しいとします, ここで は, 軸を向ける対称軸です. 円弧に作用する収束力の系は, 軸に沿った対称性により数値的に向けられた合成 Q を持ちます.

Q の値を決定するには、円弧上の要素を選択します。その位置は角度によって決まり、この要素に作用する力の長さは数値的に等しく、軸上のこの力の投影は次のようになります。

しかし、図から。 70 それ以来、それ以来、

ここで、 は円弧 AB を囲む弦の長さです。 q - 強度。

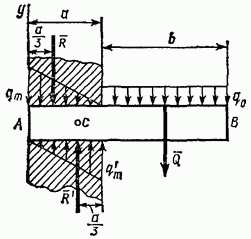
問題 27. 均一に分布した強度の荷重が片持ち梁 A B に作用し、その寸法は図に示されています (図 71)。梁の重量を無視し、埋め込まれた端にかかる圧力が次のように決定されると仮定します。線形法則に従って、これらの力の最大強度の値を決定します。

解決。 交換します 分散した力それらの結果として得られる Q、R、および R、ここで式 (35) および (36) による

ビームに作用する平行力の平衡条件 (33) を作成します。

ここでQ、R、Rの値を代入し、結果の方程式を解くと、最終的に次のことがわかります。

たとえば、いつ、いつ、

問題 28. 高さ H、内径 d の円筒にガスが圧力下で充填されており、円筒壁の厚さは a です。 これらの壁が受ける引張応力を、1) 縦方向と 2) 横方向 (応力は小さいとみなして、断面積に対する引張力の比に等しい) で決定します。

解決。 1) 円柱をその軸に垂直な平面で 2 つの部分に切り、そのうちの 1 つの部分の平衡を考えます (図 1)。

72、a）。 底部にかかる圧力と断面積全体に分布する力 (廃棄された半分の作用) によって円柱軸の方向に作用し、その合力は Q で示されます。

集中荷重間の距離は同じであり、スパンの開始点から最初の集中荷重までの距離は集中荷重間の距離に等しい。 この場合、集中荷重はスパンの最初と最後にも発生しますが、同時に増加するだけです。 支持反応、極度に集中した荷重は曲げモーメントとたわみの値にまったく影響を与えないため、計算時に 支持力構造は考慮されていません。 まぐさの上にある床梁の例を使用してこれを考えてみましょう。 レンガ造りリンテルと床梁の間にあり、同時に均一に分散された荷重を生成する可能性がありますが、理解しやすいように図示されていません。

写真1。 集中荷重を均等分布荷重と同等に軽減します。

図1からわかるように、決定的なモーメントは曲げモーメントであり、構造物の強度計算に使用されます。 したがって、均一に分散された荷重が集中荷重と同じ曲げモーメントを生成するには、適切な遷移係数 (等価係数) を掛ける必要があります。 そして、この係数はモーメントが等しいという条件から求められます。 図 1 はこれをよく示していると思います。 そして、得られた依存関係を分析することで、遷移係数を決定するための一般式を導き出すことができます。 したがって、適用される集中荷重の数が奇数の場合、つまり、 集中荷重の 1 つが必然的にスパンの中央にかかる場合、等価係数を決定するには、次の公式を使用できます。

γ = n/(n - 1) (305.1.1)

ここで、n は集中荷重間のスパンの数です。

q eq = γ(n-1)Q/l (305.1.2)

ここで、(n-1) は集中荷重の数です。

ただし、場合によっては、集中負荷の数に基づいて計算する方が便利な場合があります。 この量を変数 m で表すと、

γ = (m +1)/m (305.1.3)

この場合、等価な等分布荷重は次のようになります。

q eq = γmQ/l (305.1.4)

集中荷重の数が偶数の場合、つまり 集中荷重がスパンの中央に該当しない場合、係数の値は集中荷重の数の次の奇数として使用できます。 一般に、指定された荷重条件に従って、次の遷移係数を受け入れることができます。

γ = 2- たとえば、検討中の構造で、梁がまぐさの中央に 1 つの集中荷重のみを受ける場合。

γ = 1.33- 2 つまたは 3 つの集中荷重が作用するビームの場合。

γ = 1.2- 4 または 5 の集中荷重を受けるビームの場合。

γ = 1.142- 6 または 7 の集中荷重を受けるビームの場合。

γ = 1.11- 8 または 9 の集中荷重を受けるビームの場合。

オプション 2

集中荷重間の距離は同じですが、スパンの開始点から最初の集中荷重までの距離は、集中荷重間の距離の半分に等しくなります。 この場合、集中荷重はスパンの最初と最後にはかかりません。

図2。 集中荷重の適用の 2 番目のバリアントの移行係数の値。

図 2 からわかるように、この負荷オプションを使用すると、遷移係数の値が大幅に小さくなります。 したがって、たとえば、集中荷重が偶数の場合、遷移係数は一般に 1 に等しいと見なすことができます。 奇数の集中荷重の場合、次の公式を使用して等価係数を決定できます。

γ = (m +7)/(m +6) (305.2.1)

ここで、m は集中荷重の数です。

この場合、等価な一様分布荷重は依然として次と等しくなります。

q eq = γmQ/l (305.1.4)

一般に、指定された荷重条件に従って、次の遷移係数を受け入れることができます。

γ = 2- たとえば、検討中の構造がまぐさの中央に 1 つの集中荷重のみを受ける場合、および床梁がスパンの始点または終点にあるのか、またはスパンの始点と終点から任意に遠くに位置しているかどうか。スパン、内 この場合関係ない。 これは集中荷重を決定する際に重要です。

γ = 1- 問題の構造が偶数の荷重を受ける場合。

γ = 1.11- 3 つの集中荷重を受けるビームの場合。

γ = 1.091- 5 つの集中荷重を受けるビームの場合。

γ = 1.076- 7 つの集中荷重を受けるビームの場合。

γ = 1.067- 9 つの集中荷重を受けるビームの場合。

定義は複雑ですが、等価係数は非常にシンプルで便利です。 計算では、平方メートルまたはリニア メートルあたりに作用する分布荷重が既知であることが非常に多いため、分布荷重を最初に集中荷重に変換し、次に再度同等の分布荷重に変換しないようにするには、単に次の値を乗算するだけで十分です。適切な係数による分散荷重。 たとえば、天井には 400 kg/m2 の標準分布荷重がかかりますが、天井の自重はさらに 300 kg/m2 になります。 このとき、床梁の長さが 6 m の場合、鴨居には等分布荷重 q = 6(400 + 300)/2 = 2100 kg/m が作用します。 そして、スパンの中央に床梁が 1 つだけある場合、γ = 2、および

q eq = γq = 2q (305.2.2)

上記 2 つの条件のいずれも満たされない場合、遷移係数を純粋な形で使用することは不可能です。最初に到達しないビームまでの距離を考慮した係数をさらにいくつか追加する必要があります。まぐさのスパンの端、および集中荷重の適用が非対称になる可能性があります。 原則として、そのような係数を導き出すことは可能ですが、いずれの場合でも、最初の荷重オプションを考慮するとすべてのケースで係数が減少し、2 番目の荷重オプションを考慮すると 50% のケースで係数が減少します。 このような係数の値は次のようになります。< 1. А потому для упрощения расчетов, а заодно и для большего запаса по прочности рассчитываемой конструкции вполне хватит коэффициентов, приведенных при первых двух вариантах загружения.

分散荷重

部品、構造、機構の要素への影響は、分散荷重によって設定できます。平面システムでは、作用の強さは構造の長さに沿って設定され、空間システムでは領域全体に設定されます。

線形荷重の寸法は N/m、面積に分布する荷重の場合は N/m 2、体積荷重の場合 (たとえば、構造要素の自重を考慮する場合) - N/m 3 です。

たとえば、図 1.23 では、N/m 単位で測定された a が長さに沿って均一に分布していることが示されています。 この負荷は集中した力で置き換えることができます

Q = q ∙ AB[H]、

セグメントの途中に適用される AB.

図 1.23、b は均一に減少 (増加) する荷重を示しており、これは合力で置き換えることができます。

Q = q max ∙AB/2,

ポイントで適用される C、 そして AC = 2/3AB.

任意の場合、関数を知ることで q(x)(図 1.23、c)、等価力を計算します。

この力は、ビームの上の境界領域の重心に適用されます。 ABライン q(x).

図1.23

例としては、圧縮ガスシリンダーの壁を破壊する力の計算があります。 次の強度でパイプセクターに生じる圧力を決定してみましょう。 q[N/m]; R– パイプ半径、 2α– 中心角、軸 牛- 対称軸 (図 1.24)。

角度のある扇形要素を選択しましょう ∆φ そして強さを決める ΔQ平らな円弧要素に作用する：

∆Q = q ∙ ∆l = q ∙ R ∙ ∆φ. (1.14)

図1.24

牛意思

∆Q x = q ∙ R ∙ ∆φ ∙ cosφ. (1.15)

パイプ要素の対称性（円弧を伴う）により、 AB) 軸に対して 牛結果として生じる力の軸への投影 オイ:

Qy = 0、つまり Q = Q x, (1.16)

どこ AB円弧の両端を規定する弦です。

高さのある円筒形容器の場合 hそして内圧 P壁には強度が詰まっています q = p [N/m, 2]。 円柱を直径に沿って切断すると (図 1.25)、次のようになります。 F = q ∙ d ∙ h (d– 内径）または

F = p ∙ 2R ∙ h.

直径に沿ってシリンダーを破壊する力:

S 1 = S 2 = S;
2S = F;
S = p・h・R. (1.18)